
题目列表(包括答案和解析)
2.1 一元二次方程(1)同步练习
课时训练
 n边形的内角和:(n-2)×180°.毛
n边形的内角和:(n-2)×180°.毛
∠D+∠DAC+∠ACD=180°
∴ (∠B+∠BAC+∠ACB)+(∠D+∠DAC
(∠B+∠BAC+∠ACB)+(∠D+∠DAC +∠ACD)=180°+180°
+∠ACD)=180°+180°
∴∠B+∠D+(∠BAC+∠DAC)+(∠ACB+∠ACD)=360°
∴∠B+∠C+∠BAD+∠BCD=360°
即四边形ABCD的内角和等于360°.
∴∠PAD=180°-∠BAD=180°-120°=60°
∠PDA=180°-∠ADC=180°-105°=75°
又∵∠P+ ∠PAD+∠
∠PAD+∠ PDA=1
PDA=1 80°
80°
∴∠P=180°-∠PAD-∠PDA=180°-60°-75°=45°
 五、∵AB∥CF
五、∵AB∥CF
∴∠A=∠ACF ∠B=∠ FCD
FCD
又∵∠ ACB=∠DCE
ACB=∠DCE
∴∠A+∠B+∠C=∠ACF+∠FCD+∠DCE=180°
又∵∠A=∠C,∠B=∠B
∴∠ADB=∠CEB
 2.∵∠B+∠C+∠BAC=180°
2.∵∠B+∠C+∠BAC=180°
 ∴∠BAC=180°-∠B-∠C=180°-30°-66°=84°
∴∠BAC=180°-∠B-∠C=180°-30°-66°=84°
 又∵AD平分
又∵AD平分 ∠BAC
∠BAC
∴∠DAC=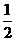 ∠BAC=
∠BAC=
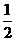 ×84°=42°
×84°=42°
∵AE⊥BC
∴∠EAC=9 0°-∠C=90°-66°=24°
0°-∠C=90°-66°=24°
∴∠DAE=∠DAC-∠EAC=42°-24°=18°
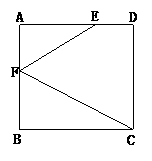
3.∵四边形ABCD是正方形
∴∠A=∠B=90°
∴∠AFE=90°-∠AEF=90°-30°=60°
∠BFC=90°-∠BCF=90°-28°=62°
∴∠EFC=180°-∠AFE-∠ BFC=180°-60°-62°=58°
BFC=180°-60°-62°=58°

答 案:
案:

五 、小
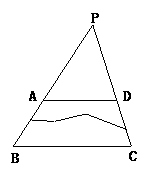
、小 明在证明“三角形内
明在证明“三角形内 角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的做法证明出来吗?
角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的做法证明出来吗?
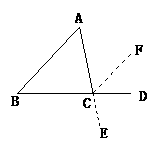
3.如图,在正方形ABCD中,已知∠AEF=30°,∠B CF=28°,求∠EFC的度数
CF=28°,求∠EFC的度数 .
.
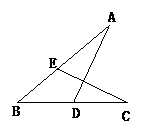
1.如图,已知: ∠A=∠C.
∠A=∠C.
求证 :∠ADB=∠CEB.
:∠ADB=∠CEB.
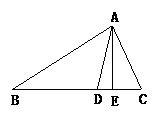
2.如图,在△ABC中,∠B=30°,∠C =65°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.[来
=65°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.[来 源:ZXXK]
源:ZXXK]
1.直角三角形的两个锐角___________.
 2.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是________三角形.
2.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是________三角形.
3.在△ABC中,∠A=∠B=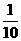 ∠C,则∠C=__
∠C,则∠C=__
 _____.
_____.
 4.在△ABC中,∠A+∠B=120°,∠A-∠B+∠C=120°,
4.在△ABC中,∠A+∠B=120°,∠A-∠B+∠C=120°, 则∠A
则∠A =_______,∠B=______.
=_______,∠B=______.
5.如图,在△ABC中,∠BAC=90°,A D⊥BC于D,则∠B=∠________,∠C=∠________
D⊥BC于D,则∠B=∠________,∠C=∠________ .
.
6.在一个三角形中,最多有______个钝角,至少有______个锐角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com