
题目列表(包括答案和解析)
2.掌握均值不等式在不等式证明中的应用。
9.直线 过点
过点 ,且分别与
,且分别与 轴,
轴, 轴的正半轴交于
轴的正半轴交于 为坐标原点:
为坐标原点:
⑴当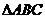 的面积最小时,求
的面积最小时,求 的方程;
的方程;
⑵当 取最小时,求
取最小时,求 的方程。
的方程。
8.一段长为L的篱笆围成一个一边靠墙的矩形菜园,问这个矩形的长,宽各为多少时,菜园面积最大,最大面积是多少?
7.⑴已知 ,求函数
,求函数 的最小值,并求
的最小值,并求 取最小值时的
取最小值时的 的值;
的值;
⑵已知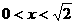 ,求函数
,求函数 的最大值,并求
的最大值,并求 取最大值时的
取最大值时的 的值。
的值。
6.填空题:
⑴若 且
且 ,则
,则
 ;
;
⑵若 且
且 则
则 ;
;
⑶若 ,则
,则 的最小值是
;
的最小值是
;
⑷函数 ,当
,当 时,
时, 有最
值是 。
有最
值是 。
5.在下列函数中,最小值是2的是………………………………………………………………( )
A.
 B.
B.
C. D.
D.
4.已知 且
且 ,则
,则 有……………………………………………………( )
有……………………………………………………( )
A.最大值64 B.最小值 C. 最小值
C. 最小值  D.
最小值64
D.
最小值64
3.已知 ,且
,且 ,则
,则 的最小值是…………………………( )
的最小值是…………………………( )
A.6 B.7 C.8 D.9
2.已知 ,且
,且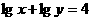 ,则
,则 的最大值是………………………………( )
的最大值是………………………………( )
A.4 B.2
C.1
D. 9
9
1.设 ,且
,且 ,则
,则 的最小值是…………………………………………( )
的最小值是…………………………………………( )
A.6
B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com