
题目列表(包括答案和解析)
18.试用定义讨论并证明函数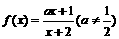 在
在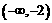 上的单调性.
上的单调性.
17.已知集合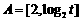 ,集合
,集合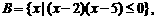
(1)对于区间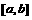 ,定义此区间的“长度”为
,定义此区间的“长度”为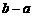 ,若A的区间“长度”为3,试求实数
,若A的区间“长度”为3,试求实数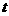 的值。
的值。
(2)若
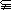
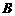 ,试求实数
,试求实数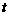 的取值范围。
的取值范围。
16.给出下面四个条件:①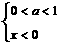 ,②
,②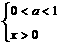 ,③
,③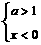 ,④
,④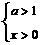 ,能使函数
,能使函数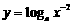 为单调减函数的是
.
为单调减函数的是
.
15.已知函数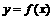 同时满足:(1)定义域为
同时满足:(1)定义域为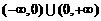 且
且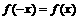 恒成立;
恒成立;
(2)对任意正实数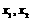 ,若
,若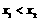 有
有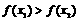 ,且
,且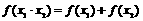 .试写出符合条件的函数
.试写出符合条件的函数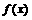 的一个解析式
的一个解析式
14.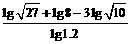 =________
=________
13.若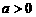 ,
,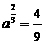 ,则
,则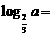 .
.
12.下表显示出函数值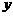 随自变量
随自变量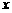 变化的一组数据,由此判断它最可能的函数模型是( ).
变化的一组数据,由此判断它最可能的函数模型是( ).
|
x |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
y |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
A.一次函数模型 B.二次函数模型 C.指数函数模型 D.对数函数模型
11.根据表格中的数据,可以断定方程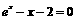 的一个根所在的区间是( ).
的一个根所在的区间是( ).
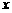 |
-1 |
0 |
1 |
2 |
3 |
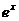 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
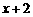 |
1 |
2 |
3 |
4 |
5 |
A. (-1,0) B. (0,1) C. (1,2) D. (2,3)
10.定义在R上的偶函数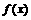 满足
满足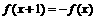 ,且当
,且当
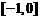 时
时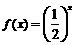 ,
,
则 等于 (
) A.
等于 (
) A. 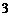 B.
B. 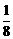 C.
C. 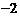 D.
D. 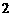
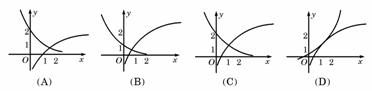
9. 函数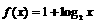 与
与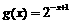 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com