
题目列表(包括答案和解析)
如图①,矩形ABCD被对角线AC分为两个直角三角形,AB=3,BC=6.现将Rt△ADC绕点C顺时针旋转90°,点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点,以BC所在直线为x轴,以过点C垂直于BC的直线为y轴,建立如图②的平面直角坐标系.
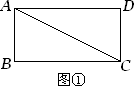
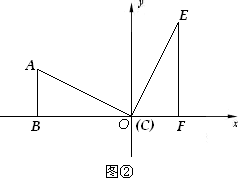
(1)求直线AE的解析式;
(2)将Rt△EFC沿x轴的负半轴平行移动,如图③.设OC=x(0<x≤9),Rt△EFC与Rt△ABO的重叠部分面积为s;
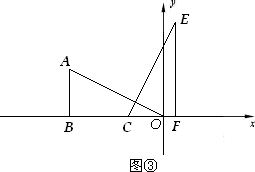
①当x=1与x=8时,分别求出s的值;
②S是否存在最大值?若存在,求出这个最大值及此时x的值;若不存在,请说明理由.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.

(1)求点B的坐标;
(2)设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;当t为何值时,△HBP的面积最大,并求出最大面积;
(3)分别以P、H为圆心,PC、HB为半径作⊙P和⊙H,当两圆外切时,求此时t的值.
【解析】(1)根据已知得出OB=OC=10,BN=OA=8,即可得出B点的坐标;
(2)利用△BON∽△POH,得出对应线段成比例,即可得出S与t之间的函数关系式;从而求出△HBP的最大面积;
(3)若⊙P和⊙H两圆外切 ,则须HB+PC=HP,从而求解
如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(6,0),(如图1).
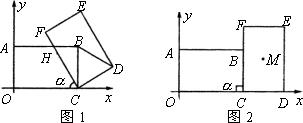
(1)当α=60°时,△CBD的形状是________;
(2)当AH=HC时,求直线FC的解析式;
(3)当α=90°时,(如图2).请探究:经过点D,且以点B为顶点的抛物线,是否经过矩形CFED的对称中心M,并说明理由.
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
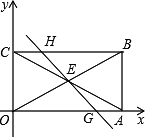
(1)①直接写出点E的坐标:________;②求证:AG=CH.
(2)如下图,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
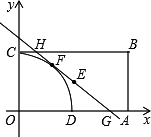
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
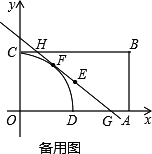
 )的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com