
有的学生一看到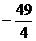 ,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
利用一元二次方程根与系数的关系易得: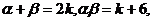

思路分析 本例只有一个答案正确,设了3个陷阱,很容易上当。
例7 设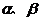 是方程
是方程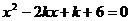 的两个实根,则
的两个实根,则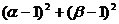 的最小值是( )
的最小值是( )
考察方程两端相应的函数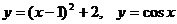 ,它们的图象无交点。
,它们的图象无交点。
所以此方程无解。
例6
解方程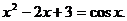
思考题:实数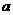 为何值时,圆
为何值时,圆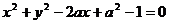 与抛物线
与抛物线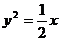 ,
,
(1) 有一个公共点;
(2) 有三个公共点;
(3) 有四个公共点;
(4) 没有公共点。
养成验算的习惯,可以有效地增强思维反思性。如:在解无理方程、无理不等式;对数方程、对数不等式时,由于变形后方程或不等式两端代数式的定义域可能会发生变化,这样就有可能产生增根或失根,因此必须进行检验,舍弃增根,找回失根。
(3) 独立思考,敢于发表不同见解
受思维定势或别人提示的影响,解题时盲目附和,不能提出自己的看法,这不利于增强思维的反思性。因此,在解决问题时,应积极地独立思考,敢于对题目解法发表自己的见解,这样才能增强思维的反思性,从而培养创造性思维。
例5 30支足球队进行淘汰赛,决出一个冠军,问需要安排多少场比赛?
解 因为每场要淘汰1个队,30个队要淘汰29个队才能决出一个冠军。因此应安排29场比赛。
思 路 分 析 传统的思维方法是:30支队比赛,每次出两支队,应有15+7+4+2+1=29场比赛。而上面这个解法没有盲目附和,考虑到每场比赛淘汰1个队,要淘汰29支队,那么必有29场比赛。
因此,当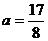 或
或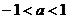 时,圆
时,圆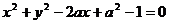 与抛物线
与抛物线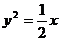 有两个公共点。
有两个公共点。
当方程①有一正根、一负根时,得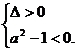 解之,得
解之,得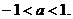
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com