
19.解:(Ⅰ)圆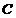 :
: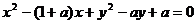 化成标准方程为:
化成标准方程为:
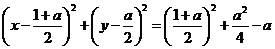 ,
,
若圆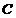 与
与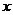 轴相切,那么有:
轴相切,那么有:
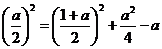 ,解得
,解得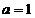 ,故所求圆
,故所求圆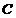 的方程为:
的方程为: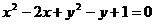 .
.
(Ⅱ)令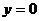 ,得
,得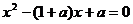 ,
,
即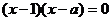 所以
所以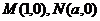
假设存在实数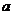 ,
,
当直线AB与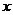 轴不垂直时,设直线AB的方程为
轴不垂直时,设直线AB的方程为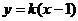 ,
,
代入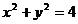 得,
得,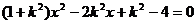 ,
,
设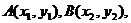 从而
从而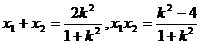
因为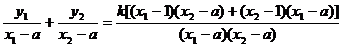
而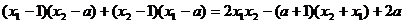
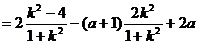
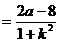
因为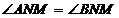 ,所以
,所以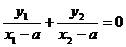 ,即
,即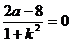 ,得
,得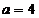 .
.
当直线AB与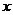 轴垂直时,也成立. 故存在
轴垂直时,也成立. 故存在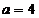 ,使得
,使得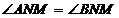 .
.
20解:设公比为q,则由题意,得q>0.
(1)①由a2-a1=8,a3=m=48,得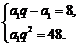
解之,得 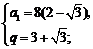 或
或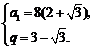
所以数列{an}的通项公式为an=8(2-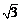 )(3+
)(3+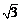 )n-1,或an=8(2+
)n-1,或an=8(2+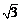 )(3-
)(3-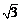 )n-1.
)n-1.
②要使满足条件的数列{an}是唯一的,即关于a1与q的方程组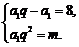 有唯一正数解,即方程8q2-mq+m=0有唯一解.
有唯一正数解,即方程8q2-mq+m=0有唯一解.
由△=m2-32m=0,a3=m>0,所以m=32,此时q=2.
经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2.
(2)由a2k+a2k-1+…+ak+1- (ak+ak-1+…+a1 )=8,
得a1(qk-1)(qk-1+qk-2+…+1)=8,且q>1.
a2k+1+a2k+2+…+a3k=a1q2k(qk-1+qk-2+…+1)
=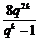 =
=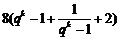 ≥32,
≥32,
当且仅当 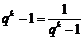 ,即q=
,即q=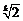 ,a1=8(
,a1=8(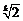 -1)时,
-1)时,
a2k+1+a2k+2+…+a3k的最小值为32.
18.解:(1)设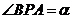 ,
,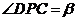 ,
,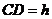 ,则
,则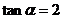 ,
,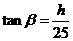 ,
,
由题意得,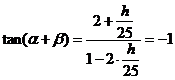 ,解得
,解得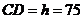 .
.
(2)设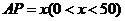 ,则
,则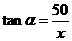 ,
,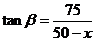 ,
,
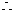
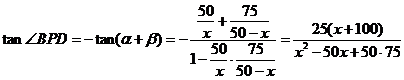 ,
,
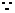
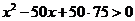 ,
,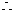
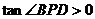 ,即
,即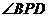 为锐角,
为锐角,
令 ,则
,则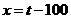 ,
,
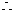
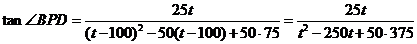 ,
,
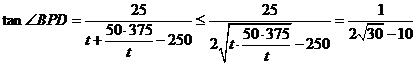 ,
,
当且仅当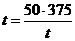 即
即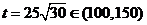 ,
,
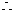
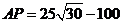 时,
时,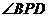 最大.
最大.
17.解:(1)因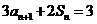 ①
①
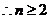 时,
时,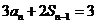 ②
②
由① - ②得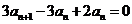 ,
,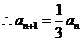
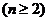
又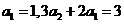 得
得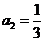 ,
,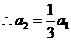
故数列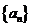 是首项为1,公比
是首项为1,公比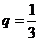 的等比数列,
的等比数列,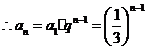
(2)假设存在满足题设条件的实数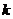 ,由(1)知
,由(1)知
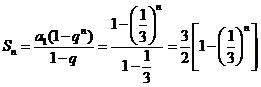
由题意知,对任意正整数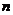 恒有
恒有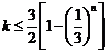 ,又数列
,又数列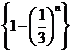 单调递增,
单调递增,
所以,当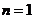 时数列中的最小项为
时数列中的最小项为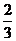 ,则必有
,则必有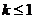 ,即实数
,即实数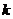 最大值为1.
最大值为1.
二、解答题
16.解:(1)由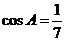
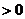
 ,
,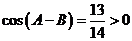 ,得
,得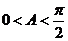 且
且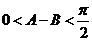 ,
,
可得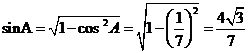 ,
,
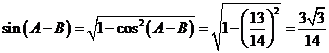 ,
,
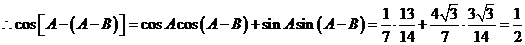 ,
,
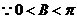 ,
,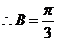 ,
, 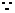 在
在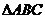 中,
中,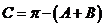 ,
,
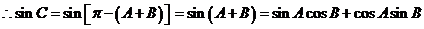
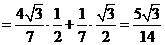 ;
;
(2)在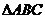 中,由正弦定理得:
中,由正弦定理得: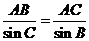 ,
,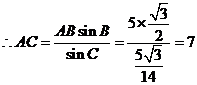 .
.
10.-3 11. 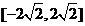 12.1
13.
12.1
13.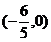 14.2101
14.2101
5.10100 6.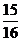 7.
7.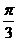 8.
8. 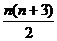 9.
π-2
9.
π-2
一、填空题
1.3x-4y+8=0或3x+4y-8=0 2. 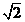 3.-6 4.(x+2)2+2=
3.-6 4.(x+2)2+2=
20.(本小题满分1 6分)已知数列{an}成等比数列,且an>0.
6分)已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.
①当m=48时,求数列{an}的通项公式;
②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+…+ak+1- (ak+ak-1+…+a1 )=8,k∈N*,
求a2k+1+a2k+2+…+a3k的最小值.
高一第二学期数学期末考试模拟试卷(答案)
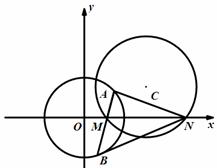
19.(本小题满分1 6分)如图,圆
6分)如图,圆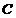 :
: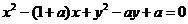 .(Ⅰ)若圆
.(Ⅰ)若圆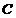 与
与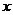 轴相切,求圆
轴相切,求圆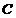 的方程;(Ⅱ)已知
的方程;(Ⅱ)已知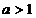 ,圆C与
,圆C与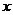 轴相交于两点
轴相交于两点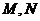 (点
(点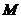 在点
在点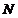 的左侧).过点
的左侧).过点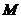 任作一条直线与圆
任作一条直线与圆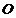 :
: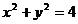 相交于两点
相交于两点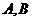 .问:是否存在实数
.问:是否存在实数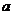 ,使得
,使得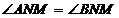 ?若存在,求出实数
?若存在,求出实数 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

18.(本小题满分16分)图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔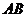 、
、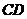 与桥面
与桥面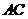 垂直,通过测量得知
垂直,通过测量得知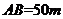 ,
,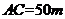 ,当
,当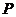 为
为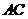 中点时,
中点时,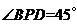 .(1)求
.(1)求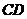 的长;(2)试问
的长;(2)试问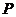 在线段
在线段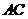 的何处时,
的何处时,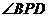 达到最大.
达到最大.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com