
18.(本小题满分12分)
在直角坐标系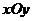 中,已知点
中,已知点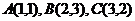 ,点
,点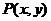 在
在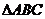 三边围成的
三边围成的
区域(含边界)上.
(Ⅰ)若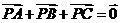 ,求
,求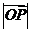 ;
;
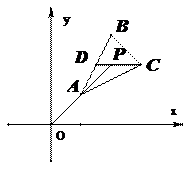 (Ⅱ)设
(Ⅱ)设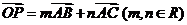 ,用
,用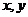 表示
表示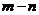 ,并求
,并求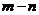 的最大值.
的最大值.
解:(Ⅰ)如图,取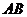 的中点
的中点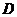 ,则
,则
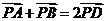 ,∴
,∴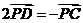 ,
,
因此,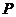 是
是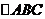 的重心,
的重心,
所以,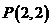 ,
,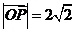 .
.
(Ⅱ)(Ⅱ)由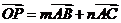 ,得
,得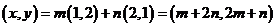 ,
,
 ∴
∴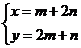 ,∴
,∴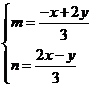 ,
,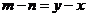 ,
,
设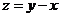 ,
,
如图,直线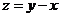 过点
过点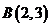 时,
时,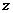 取得
取得
最大值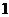 ,即
,即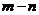 的最大值为
的最大值为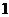 .
.
17. (本小题满分12分)
(本小题满分12分)
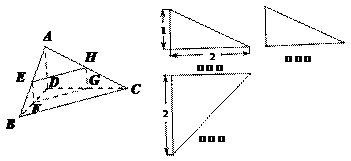
四面体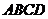 及其三视图如图所示,
及其三视图如图所示,
过被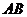 的中点
的中点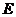 作平行于
作平行于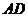 ,
,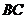 的
的
平面分别交四面体的棱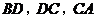 于
于
点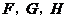 .
.
(I)证明:四边形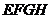 是矩形;
是矩形;
(II)求直线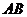 与平面
与平面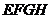 夹角
夹角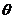 的正弦值.
的正弦值.
(Ⅰ)证明:∵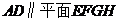 ,
,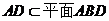 ,且
,且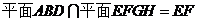 ,∴
,∴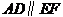 ,同理
,同理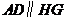 ,∴
,∴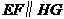 ,
,
由 同理可得
同理可得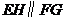 ,∴四边形
,∴四边形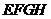 是平行四边形.
是平行四边形.
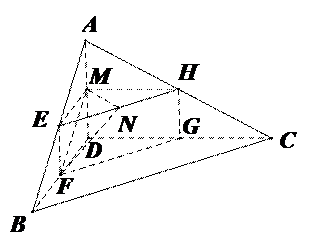 由三视图知
由三视图知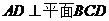 ,又
,又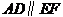 ,∴
,∴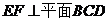 ,
,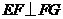 ,
,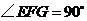 ,
,
所以四边形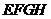 是矩形.
是矩形.
(II)解:取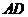 的中点
的中点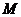 ,连结,
,连结,
显然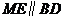 ,
,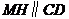 ,
,
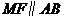 ,且
,且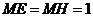 ,
,
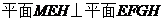 ,
,
取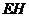 的中点
的中点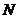 ,连结
,连结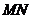 ,
,
则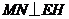 ,
,
∴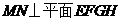 ,则
,则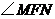 就是
就是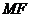 (即
(即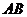 )与平面
)与平面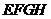 所成的角
所成的角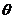 ,
,
∵三角形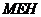 是等腰直角三角形,∴
是等腰直角三角形,∴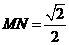 ,
,
又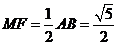 ,∴
,∴ ,
,
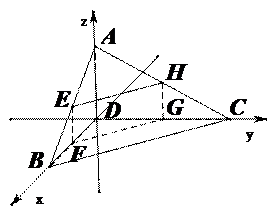 即直线
即直线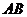 与平面
与平面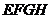 夹角
夹角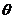 的正弦值是
的正弦值是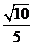 .
.
(向量法)建立坐标系如图,
由条件可得,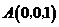 ,
,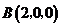 ,
,
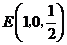 ,
,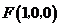 ,
,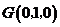 ,
,
则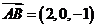
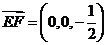 ,
,
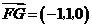 ,设平面
,设平面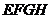 的法向量
的法向量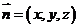 ,则
,则
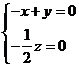 ,取
,取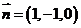 ,则
,则
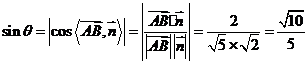 .
.
三、解答题:解答应写出文字说明、证明过程或演算步骤
16. (本小题满分12分)
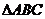 的内角
的内角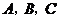 所对的边分别为
所对的边分别为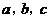 .
.
(I)若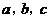 成等差数列,证明:
成等差数列,证明: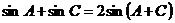 ;
;
(II)若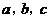 成等比数列,求
成等比数列,求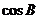 的最小值.
的最小值.
解:(Ⅰ)证明:∵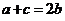 ,∴
,∴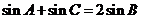 ,又
,又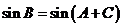 ,
,
∴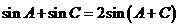 .
.
(Ⅱ)∵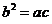 ,
,
∴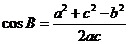
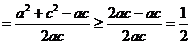 .
.
所以当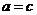 时,
时,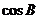 的最小值为
的最小值为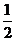 .
.
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
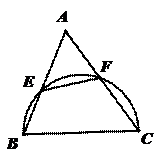
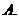 (不等式选做题)设
(不等式选做题)设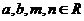 ,且
,且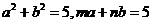 ,则
,则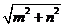 的最小值为
的最小值为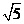
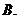 (几何证明选做题)如图,
(几何证明选做题)如图,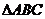 中,
中,
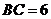 ,以
,以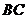 为直径的半圆分别交
为直径的半圆分别交
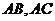 于点
于点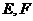 ,若
,若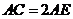 ,
,
则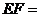
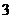 .
.
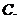 (坐标系与参数方程选做题)在极坐标系中,点
(坐标系与参数方程选做题)在极坐标系中,点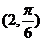 到直线
到直线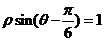 的距离是
的距离是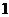 .
.
14. 观察分析下表中的数据:
|
多面体 |
面数(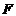 ) ) |
顶点数(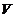 ) ) |
棱数(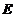 ) ) |
|
三棱锥 |
5 |
6 |
9 |
|
五棱锥 |
6 |
6 |
10 |
|
立方体 |
6 |
8 |
12 |
猜想一般凸多面体中,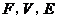 所满足的等式是
所满足的等式是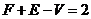 .
.
13. 设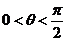 ,向量
,向量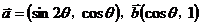 ,若
,若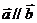 ,则
,则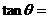
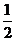 .
.
14.若圆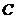 的半径为1,其圆心与点
的半径为1,其圆心与点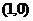 关于直线
关于直线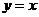 对称,则圆
对称,则圆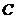 的标准方程为
的标准方程为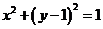 .
.
三、填空题:把答案填写在答题卡相应题号后的横线上.
13.已知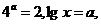 则
则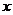 =
=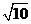 .
.
10. 如图,某飞行器在4千米高空水平飞行,从距着陆点
如图,某飞行器在4千米高空水平飞行,从距着陆点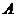 的水平距离10千米处下降, 已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为
( A )
的水平距离10千米处下降, 已知下降飞行轨迹为某三次函数图像的一部分,则函数的解析式为
( A )
(A)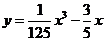
(B)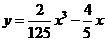
(C)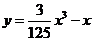
(D)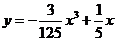
10.设样本数据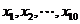 的均值和方差分别为1和4,若
的均值和方差分别为1和4,若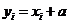 (
(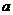 为非零常数,
为非零常数, 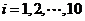 ),则
),则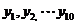 的均值和方差分别为
( A )
的均值和方差分别为
( A )
(A)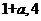 (B)
(B)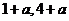 (C)
(C)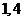 (D)
(D)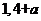
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com