
4.下列性质中,菱形具有,矩形不一定具有的是  ( )
( )
A.四个角为直角 B.对角线互相垂直 C.对角线相等 D.对角 相等
相等
3.下面能构成直角三角形的三边长是 ( )
A. 2 ,3 ,4 B. 4 ,5 ,9
C. 5,13,12 D. 8 ,6 ,4
2.顺次连结菱形各边中点所得的图形是 ( )
A.平行四边形 B.菱形 C.矩形 D.正方形
一、选择
1.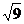 = ( )
= ( )
A. ±3 B. 3 C . — 3 D . 9
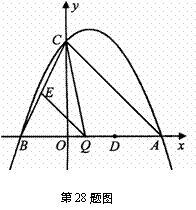
28.(本题满分12分)
已知:如图,在平面直角坐标系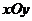 中,二次函数
中,二次函数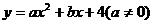 与
与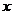 轴交于点
轴交于点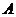 、
、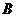 ,点
,点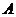 的坐标为
的坐标为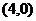 ,点
,点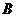 的坐标为
的坐标为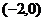 .
.
(1)求该二次函数的表达式;
(2)点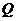 是线段
是线段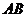 上的动点,过点
上的动点,过点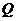 作
作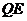 ∥
∥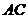 ,交
,交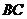 于点
于点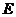 ,连接
,连接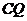 .
.
当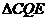 的面积最大时,求点
的面积最大时,求点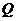 的坐标;
的坐标;
(3)若平行于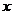 轴的动直线
轴的动直线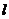 与该抛物线交于点
与该抛物线交于点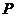 ,与直线
,与直线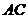 交于点
交于点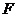 ,点
,点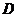 的坐标为
的坐标为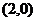 .问:是否存在这样的直线
.问:是否存在这样的直线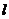 ,使得
,使得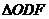 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点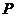 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
27.(本题满分12分)
 将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片
将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片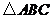 和
和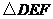 .将这两张三角形胶片的顶点
.将这两张三角形胶片的顶点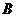 与顶点
与顶点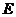 重合,把
重合,把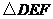 绕点
绕点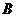 顺时针方向旋转,这时
顺时针方向旋转,这时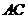 与
与 相交于点
相交于点 .
.
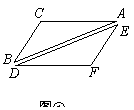
(1) 当 旋转至如图②位置,点
旋转至如图②位置,点 ,
, 在同一直线上时,
在同一直线上时,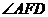 与
与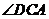 的数量关系是 ▲
.
的数量关系是 ▲
.
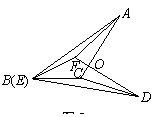
(2)当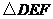 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接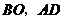 ,探索
,探索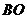 与
与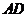 之间有怎样的位置关系,并证明.
之间有怎样的位置关系,并证明.
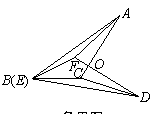
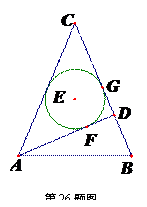
26.(本题满分10分)
如图,在等腰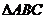 中,CA=CB,AD是腰BC边上的高,
中,CA=CB,AD是腰BC边上的高,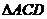 的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
(1)求证:AF=BG;
(2)过E点作EH⊥AB于H,试探索线段EH与线段AB的数量关系,并说明理由.
25.(本题满分10分)
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为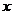 元(
元(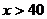 ),请你分别用
),请你分别用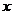 的代数式来表示销售量
的代数式来表示销售量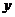 件和销售该品牌玩具获得利润
件和销售该品牌玩具获得利润 元,并把结果填写在表格中:
元,并把结果填写在表格中:
|
销售单价(元) |
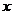 |
销售量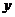 (件) (件) |
|
销售玩具获得利润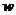 (元) (元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价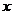 应定为多少元?
应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
24.(本题满分10分)
 如图,为了测量某建筑物
如图,为了测量某建筑物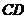 的高度,先在地面上用测角仪自
的高度,先在地面上用测角仪自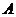 处测得建筑物顶部的仰角是
处测得建筑物顶部的仰角是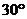 ,然后在水平地面上向建筑物前进了
,然后在水平地面上向建筑物前进了 ,此时自
,此时自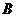 处测得建筑物顶部的仰角是
处测得建筑物顶部的仰角是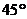 .已知测角仪的高度是
.已知测角仪的高度是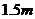 ,请你计算出该建筑物的高度.(取
,请你计算出该建筑物的高度.(取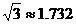 ,结果精确到
,结果精确到 )
)
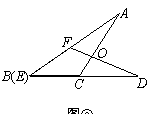
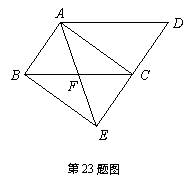
23.(本题满分10分)
如图,将□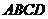 的边
的边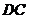 延长到点
延长到点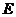 ,使
,使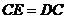 ,连接
,连接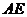 ,交
,交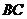 于点
于点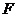 .
.
(1)求证: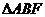 ≌
≌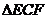 ;
;
(2)若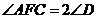 ,连接
,连接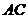 、
、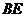 .求证:四边形
.求证:四边形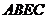 是矩形.
是矩形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com