
5、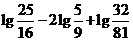 等于
等于
A、lg2 B、lg3 C、lg4 D、lg5
4、设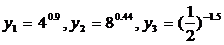 ,则
,则
A、y3>y1>y2 B、y2>y1>y3 C、y1>y2>y3 D、y1>y3>y2
3、函数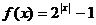 ,使
,使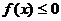 成立的
成立的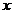 的值的集合是
的值的集合是
A、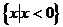 B、
B、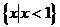 C、
C、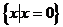 D、
D、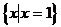
2、函数y=5x+1的反函数是
A、y=log5(x+1) B、y=logx5+1 C、y=log5(x-1) D、y=log(x+1)5
一、选择题:
1、化简[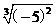 ]
]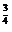 的结果为
的结果为
A、5 B、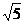 C、-
C、-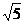 D、-5
D、-5
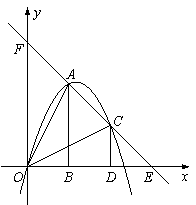
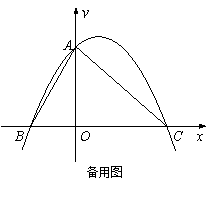
2、如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F,抛物线y=ax 2+bx+c经过O、A、C三点.
(1)求该抛物线的函数解析式;
(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
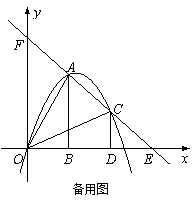
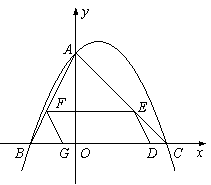
1、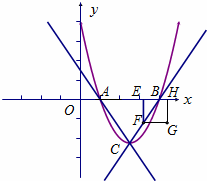 如图,二次函数y=x2-5x+4的图象与x轴交于A,B两点(点A在点B左侧),顶点为C,有一个动点E从点B出发以每秒一个单位向点A运动,过E 作y轴的平行线,交△ABC的边BC或AC于点F,以EF为边在EF右侧作正方形EFGH,设正方形EFGH与△ABC重叠部分面积为S,E点运动时间为t秒.
如图,二次函数y=x2-5x+4的图象与x轴交于A,B两点(点A在点B左侧),顶点为C,有一个动点E从点B出发以每秒一个单位向点A运动,过E 作y轴的平行线,交△ABC的边BC或AC于点F,以EF为边在EF右侧作正方形EFGH,设正方形EFGH与△ABC重叠部分面积为S,E点运动时间为t秒.
(1)求顶点C的坐标和直线AC的解析式;
(2)求当点F在AC边上,G在BC边上时t的值;
(3)求动点E从 点B向点A运动过程中,S关于t的函数关系
点B向点A运动过程中,S关于t的函数关系
28.(本题满分12分)
如图,抛物线与x轴交于点B(-2,0)、C(4,0),与y轴正半轴交于点A,且tan∠ABC=2.
(1)求该抛物线的解析式;
(2)□DEFG的一边DG在线段BC上,另两个顶点E、F分别在线段AC和线段AB上,且
∠EFG=∠ABC,若点D的坐标为(m,0),□DEFG的面积为S,求S与m的函数关系式,并求出S的最大值;
 (3)点N在线段BC上运动,连接AN,将△ANC沿直线AC翻折得到△AN ′C,AN ′ 与抛物线的另一个交点为M,若点M恰好将线段AN ′ 分成1 : 3两部分,求点N的坐标.
(3)点N在线段BC上运动,连接AN,将△ANC沿直线AC翻折得到△AN ′C,AN ′ 与抛物线的另一个交点为M,若点M恰好将线段AN ′ 分成1 : 3两部分,求点N的坐标.
压轴题备选题
27.(本题满分12分)
课外活动小组活动时,陈老师提出了如下问题:
已知:如图1,在△ABC中,∠ABC=∠ACB=α,点D是AB边上任意一点,将射线DC绕点D逆时针旋转α与过点A且平行于BC边的直线交于点E.当α=60°时 ,请判断线段BD与AE之间的数量关系.
,请判断线段BD与AE之间的数量关系.
小明在小组内经过合作交流,得到了如下的解决方法:过D点作AC的平行线交BC于F,构造全等三角形,通过推理使得问题得解.
(1)写出原问题BD与AE之间的数量关系,并写出证明过程.
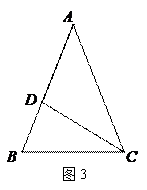 (2)如图2,在原问题条件下当α=45°时,判断线段BD与AE之间的数量
(2)如图2,在原问题条件下当α=45°时,判断线段BD与AE之间的数量 关系,并进行证明;(3)如图3,在原问题条件下当α为任意锐角时,依题意补全图形,请直接写出线段BD与AE之间的数量关系:_______________________.(用含α的式子表示,其中
关系,并进行证明;(3)如图3,在原问题条件下当α为任意锐角时,依题意补全图形,请直接写出线段BD与AE之间的数量关系:_______________________.(用含α的式子表示,其中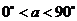 )
)

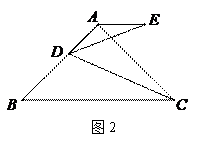
26.(本题满分10分)
根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2014年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
|
一户居民一个月用电量的范围 |
电费价格(单位:元/千瓦时) |
|
不超过200千瓦时 |
a |
|
超过200千瓦时但不超过350千瓦时的部分 |
b |
|
超过350千瓦时的部分 |
a+0.3 |
2014年5月份,该市居民甲用电100千瓦时,交电费50元;居民乙用电300千瓦时,交电费160元.该市一户居民在2014年5月以后,某月用电 千瓦时,当月交电费
千瓦时,当月交电费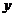 元.
元.
(1)上表中,a=  ;b= ;
;b= ;
(2)请求出 与
与 之间的函数关系式;
之间的函数关系式;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.52元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com