8．(2014·云南部分名校统考)如图7所示，与水平面夹角为θ＝30°的倾斜传送带始终绷紧，传送带下端A点与上端B点间的距离为L＝4 m，传送带以恒定的速率v＝2 m/s向上运动．

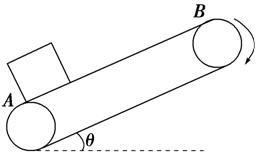
图7

现将一质量为1 kg的物体无初速度地放于A处，已知物体与传送带间的动摩擦因数μ＝，取g＝10 m/s²，求：

(1)物体从A运动到B共需多少时间？

(2)电动机因传送该物体多消耗的电能．

[解析]　(1)物体无初速度放在A处后，因mgsin θ<μmgcos θ，则物体斜向上做匀加速直线运动，

加速度a＝＝2.5 m/s²

物体达到与传送带同速所需的时间t₁＝＝0.8 s

t₁时间内物体的位移L₁＝t₁＝0.8 m

之后物体以速度v₁做匀速运动，运动的时间t₂＝＝1.6 s

物体运动的总时间t＝t₁＋t₂＝2.4 s

(2)前0.8 s内物体相对传送带的位移为ΔL＝vt₁－L₁＝0.8 m

因摩擦而产生的内能E_内＝μmgcos θ·ΔL＝6 J

E_总＝E_k＋E_p＋E_内＝mv²＋mgLsin θ＋E_内＝28 J

[答案]　(1)2.4 s　(2)28 J

7．如图6所示，一质量为m＝0.5 kg的小滑块，在F＝4 N水平拉力的作用下，从水平面上的A处由静止开始运动，滑行s＝1.75 m后由B处滑上倾角为37°的光滑斜面，滑上斜面后拉力的大小保持不变，方向变为沿斜面向上，滑动一段时间后撤去拉力．

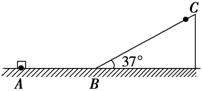
图6

已知小滑块沿斜面上滑到的最远点C距B点为l＝2 m，小滑块最后恰好停在A处．不计B处能量损失，g取10 m/s²，已知sin 37°＝0.6，cos 37°＝0.8.试求：

(1)小滑块与水平面间的动摩擦因数μ；

(2)小滑块在斜面上运动时，拉力作用的距离x；

(3)小滑块在斜面上运动时，拉力作用的时间t.

[解析]　(1)小滑块由C点运动到A点，由动能定理得mglsin 37°－μmgs＝0解得μ＝.

(2)小滑块由A点运动到C点，由动能定理得F(s＋x)－mglsin 37°－μmgs＝0解得x＝1.25 m.

(3)小滑块由A点运动到B点，由动能定理得Fs－μmgs＝mv²；由牛顿第二定律得F－mgsin 37°＝ma；由运动学公式得x＝vt＋at²；联立各式，解得t＝0.5 s.

[答案]　(1)　(2)1.25 m　(3)0.5 s

6．(多选)一质量为1 kg的物体，以10 m/s的初速度从足够长的粗糙斜面上的A点沿斜面向上运动，1 s末物体恰好到达最高点，6 s末物体的速率恰好为10 m/s，则(　)

A．1 s～6 s内物体所受重力的平均功率为50 W

B．6 s末物体克服摩擦力做功的瞬时功率为20 W

C．0～1 s内物体机械能的变化量大小与1 s～6 s内机械能的变化量大小之比为1∶5

D．1 s～6 s内物体动能变化量的大小与机械能的变化量大小之比是1∶2

[解析]　由题意可知，物体沿斜面方向上的加速度由摩擦力f和重力沿斜面向下的分力F提供，设沿斜面方向向下为正方向，由牛顿第二定律结合运动学规律有F＋f＝ma₁，F－f＝ma₂，a₁＝＝10 (m/s²)，a₂＝＝2 (m/s)²，解得f＝4 N，F＝6 N．1 s～6 s内，克服摩擦力做的功为W_f＝fs₂，s₂＝，解得W_f＝100 J，据动能定理可得W_G－W_f＝ΔE_k＝50 J，解得W_G＝150 J，故1 s～6 s内物体所受重力的平均功率为P＝＝30 W，A错误.

6 s末物体克服摩擦力做功的瞬时功率为40 W，B错误．由题意可知摩擦力做的功等于物体机械能的变化，0～1 s内和1 s～6 s内物体的位移大小为5 m和25 m，故0～1 s内物体机械能的变化量大小与1 s～6 s内机械能的变化量大小之比为1∶5，C正确.1 s～6 s内物体动能变化量的大小等于50 J，机械能的变化量大小等于100 J，故D正确．

[答案]　CD

5．(多选)如图5所示，放置在竖直平面内的光滑杆AB，是按照从高度为h处以初速度v₀平抛的运动轨迹制成的，A端为抛出点，B端为落地点．现将一小球套于其上，由静止开始从轨道A端滑下．已知重力加速度为g，当小球到达轨道B端时(　)

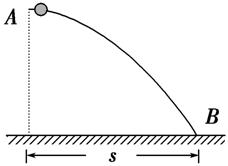
图5

A．小球的速率为

B．小球的速率为

C．小球在水平方向的速度大小为v₀.

D．小球在水平方向的速度大小为

[解析]　由机械能守恒定律，mgh＝mv²，解得小球到达轨道B端时速率为v＝，选项A错误，B正确．设轨道在B点切线方向与水平方向的夹角为α，则有cot α＝，cos α＝.小球在水平方向的速度大小为v₁＝vcos α＝＝，选项D正确，C错误．

[答案]　BD

4．如图4所示，A、B两小球由绕过轻质定滑轮的细线相连，A放在固定的光滑斜面上，B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连，C球放在水平地面上．

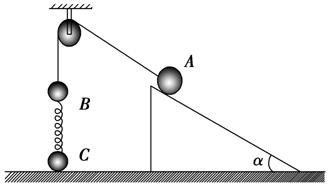
图4

现用手控制住A，并使细线刚刚拉直但无拉力作用，并保证滑轮左侧细线竖直、右侧细线与斜面平行．已知A的质量为4m.B、C的质量均为m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放A后，A沿斜面下滑至速度最大时C恰好离开地面．下列说法正确的是(　)

A．斜面倾角α＝60°

B．A获得最大速度为2g

C．C刚离开地面时，B的加速度最大

D．从释放A到C刚离开地面的过程中，A、B两小球组成的系统机械能守恒

[解析]　释放A后，A沿斜面下滑至速度最大时拉力等于A重力沿斜面分力4mgsin α，C恰好离开地面，轻质弹簧弹力等于C球重力，kx＝mg.对B，由平衡条件，4mgsin α＝2mg，解得斜面倾角α＝30°，选项A错误；初状态，弹簧压缩，kx＝mg.末状态，弹簧拉伸，kx＝mg.初末状态系统弹簧弹性势能相等，由机械能守恒定律，4mg·2xsin α－mg2x＝(m＋4m)v²，解得v＝2g，选项B正确；

C刚离开地面时，B的加速度为零，选项C错误；从释放A到C刚离开地面的过程中，A、B、C和弹簧组成的系统机械能守恒，选项D错误．

[答案]　B

3.将一小球从高处水平抛出，最初2 s内小球动能E_k随时间t变化的图线如图3所示，不计空气阻力，重力加速度g＝10 m/s².根据图象信息，不能确定的物理量是(　)

A．小球的质量

B．小球的初速度

C．最初2 s内重力对小球做功的平均功率

D．小球抛出时的高度

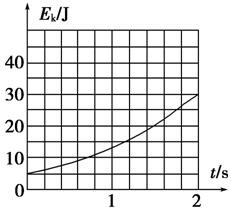
图3

[解析]　小球平抛初动能为5 J，可得mv²＝5 J,2 s末小球竖直速度为gt＝20 m/s,2 s末小球动能m(v＋20²)＝30 J，联立可解得小球的质量和初速度．最初2 s内重力对小球做功mgh＝mg·gt²，由P＝W/t可以确定最初2 s内重力对小球做功的平均功率．不能确定小球抛出时的高度．

[答案]　D

2.如图2所示，一高度为h的楔形物块固定在水平地面上，质量为m的物体由静止开始从倾角分别为α、β的两个光滑斜面的顶端滑下，则下列说法中正确的是(　)

A．物体滑到斜面底端的速度相同

B．物体滑到斜面底端所用的时间相同

C．物体滑到斜面底端时重力所做功的功率相同

D．物体滑到斜面底端过程中重力所做的功相同

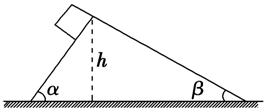
图2

[解析]　由机械能守恒定律，物体沿不同倾角的光滑斜面滑到斜面底端的速度大小相等，方向不相同，选项A错误；物体滑到斜面底端所用的时间不相同，选项B错误；物块滑到斜面底端过程中重力所做的功相同，所用时间不同，物体滑到斜面底端时重力所做功的功率不相同，选项C错误，D正确．

[答案]　D

1．质量为m的物体静止在粗糙的水平地面上．现用一水平拉力使物体从静止开始运动，其运动的v－t图象如图1所示．下列关于物体运动过程，分析正确的是(　)

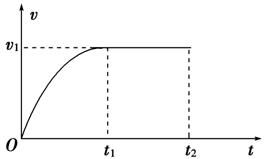
图1

A．0～t₁内拉力逐渐减小

B．0～t₁内拉力对物体做负功

C．在t₁～t₂时间内拉力的功率为零

D．在t₁～t₂时间内合外力做功为mv

[解析]　由v－t图象可知，0～t₁内斜率逐渐变小，物体的加速度逐渐减小，由牛顿第二定律知，拉力逐渐减小；0～t₁内物体的速率一直增加，合力做功大于零，所以拉力对物体一直做正功；t₁～t₂时间内，物体做匀速运动，拉力的功率等于摩擦力的功率，但不等于零，合外力做功为零．只有A对．

[答案]　A

2．(2014·厦门一中模拟)在某电视台游乐节目“闯关”中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，如图5－4所示．

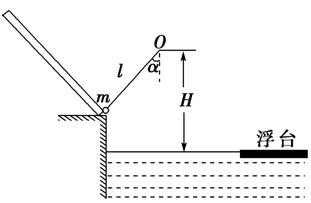
图5－4

一选手先从倾角可调整的光滑斜面下滑到悬绳处，然后抓住绳开始摆动，摆动到最低点放手恰能到达浮台．此绳初始时与竖直方向夹角α＝30°，与斜面垂直，绳长l＝2 m，绳的悬挂点O距水面的高度为H＝3 m．将选手简化为质量m＝60 kg的质点，不考虑空气阻力和绳的质量，浮台离绳的悬挂点水平距离为4 m，露出水面的高度不计，水足够深．取重力加速度g＝10 m/s².

(1)求选手在斜面上下滑的高度h；

(2)求选手摆到最低点时对绳拉力的大小F；

(3)如果斜面的倾角增大，该选手下滑高度不变，选手仍摆动到最低点放手，能否到达浮台？请说明理由．

[解析]　(1)设选手滑到斜面底端的速度为v₁，由机械能守恒得mgh＝mv

选手抓绳时速度与绳垂直，抓绳后速度不变，摆到最低点时的速度为v₂，由机械能守恒得mgl(1－cos α)＝mv－mv

选手放手后做平抛运动，下落时间为t，水平距离为s＝4 m，由平抛运动规律得t＝，s＝v₂t[来源:Z。X。X。K]

联立求得：h＝(2＋)m＝3.73 m，v₂＝4 m/s.

(2)选手在最低点时，由牛顿运动定律得F－mg＝，解得F＝3 000 N.

(3)不能．如果斜面倾角增大，选手下滑到底端时的速度为v₃，如图所示在沿绳和垂直于绳方向上的分量为v₄、v₅，选手抓绳后v₄消失，只剩v₅，小于v₃，即小于v₁，选手仍摆动到最低点放手水平速度小于v₂，不能到达浮台．(只要理由充分，其他解答也对)

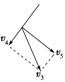
[答案]　见解析

动能定理或能量守恒在系统中的巧妙应用

　总质量为M的列车，沿水平直线轨道匀速前进，其末节车厢质量为m，中途脱节，司机发觉时，列车已行驶的距离为L，于是立即关闭油门，除去牵引力．设运动的阻力与质量成正比，机车的牵引力是恒定的．当列车的两部分都停止时，它们的距离是多少？

[技法攻略]　若脱钩的同时关闭油门，则列车和末节车厢将同时停止下来，且停下来时二者间距为零(因二者始、末速度以及减速的加速度都相同)．现在的情况是牵引力多做功FL，因此列车一定多前进一段Δs，克服其摩擦力做功k(M－m)gΔs才能停下来．

故有：FL＝k(M－m)gΔs

又由于原来列车匀速前进，得出F＝kMg

解得：Δs＝.

[答案]　

　(多选)如图5－5所示，固定在竖直面内的光滑圆环半径为R，圆环上套有质量分别为m和2m的小球A、B(均可看做质点)，且小球A、B用一长为2R的轻质细杆相连，在小球B从最高点由静止开始沿圆环下滑至最低点的过程中(已知重力加速度为g)，下列说法正确的是(　)

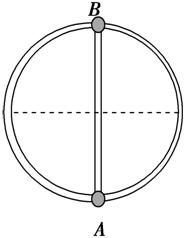
图5－5

A．A球增加的机械能等于B球减少的机械能

B．A球增加的重力势能等于B球减少的重力势能

C．A球的最大速度为

D．细杆对A球做的功为mgR

[技法攻略]　系统机械能守恒可以理解为是一种机械能的转移，此题的情境就是A球增加的机械能等于B球减少的机械能，A对，B错；根据机械能守恒定律：2mg·2R－mg·2R＝·3mv²，所以A球的最大速度为 ，C错；根据功能关系，细杆对A球做的功等于A球增加的机械能，即W_A＝mv²＋mg·2R＝mgR，故D对．

[答案]　AD

1.如图5－2所示，轻质弹簧的一端与固定的竖直板P拴接，另一端与物体A相连，物体A置于光滑水平桌面上，A右端连接一细线，细线绕过光滑的定滑轮与物体B相连．开始时托住B，A处于静止且细线恰好伸直，然后由静止释放B，直至B获得最大速度．下列有关该过程的分析中正确的是

(　)

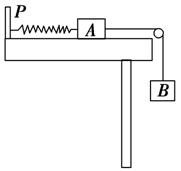
图5－2

A．B物体受到细线的拉力保持不变

B．B物体机械能的减少量小于弹簧弹性势能的增加量

C．A物体动能的增加量等于B物体的重力对B做的功与弹簧弹力对A做的功之和

D．A物体与弹簧所组成的系统机械能的增加量等于细线拉力对A做的功

[解析]　由静止释放B直至B获得最大速度的过程中，由于弹簧随着A、B一起运动导致弹力变大，所以A、B的合力以及加速度都在减小，速度增大，B物体受到细线的拉力一直在增大，A错；B物体机械能的减少量等于弹簧弹性势能的增加量和A的动能的增加量之和，故B项也错；根据动能定理可知A物体动能的增加量等于细线对A做的功与弹簧弹力对A做功的代数和，C错；根据功能关系可判断D项说法正确．

[答案]　D

巧妙建立物理模型

物理学上建立模型，是为了将问题简化，突出主要矛盾，忽略次要因素．物理模型有实体模型如质点、点电荷，有过程模型，如匀速运动、匀变速运动、匀速圆周运动、平抛运动等，有状态模型，如平衡状态、加速状态等．

　如图5－3所示，水平传送带AB的右端与竖直面内的光滑半圆形轨道DC相接．传送带的运行速度为v₀＝8 m/s，将质量m＝1.0 kg的滑块无初速度地放到传送带A端．

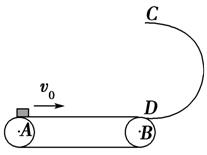
图5－3

已知传送带长度L＝12.0 m，竖直面内的光滑半圆形轨道的半径R＝0.8 m，滑块与传送带间的动摩擦因数为μ＝0.4，重力加速度g＝10 m/s².试求：

(1)滑块从传送带A端运动到B端所需的时间；

(2)滑块在传送带上滑行的整个过程中产生的热量；

(3)滑块滑到轨道最高点C时对轨道的压力．

[解析]　(1)滑块在传送带上做加速运动的加速度a＝μg＝4 m/s²

加速到与传送带同速所用时间t₁＝＝2 s

位移x₁＝at＝8 m＜12 m，因此滑块在传送带上先做加速运动，后做匀速运动，做匀速运动的位移x₂＝L－x₁＝4 m

所用时间t₂＝＝0.5 s

故t＝t₁＋t₂＝2.5 s.

(2)在t₁时间内，传送带的位移x′＝v₀t₁＝16 m

故Q＝fΔx＝μmg(x′－x₁)＝32 J.

(3)滑块由D到C过程中机械能守恒，则

mg(2R)＋mv＝mv

在C点，轨道对滑块的弹力与滑块重力的合力提供向心力

则N＋mg＝，解得N＝30 N.

由牛顿第三定律得滑块对轨道的压力N′＝N＝30 N，方向竖直向上．

[答案]　见解析

[即学即用]