
1.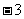 的相反数是
的相反数是
A. B.
B.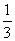 C.
C.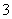 D.
D.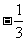
24.(本题满分9分)
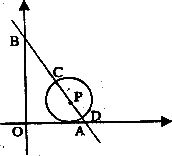
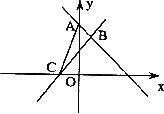
如图,在平面直角坐标系中,直线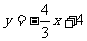 分别交
分别交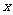 轴
轴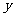 轴于A、B亮点.
轴于A、B亮点.
(1)求A、B两点坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和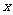 的轴相切,和直线AB交于C、D两点(点C的横坐标小于点D的横坐标),设P点的横坐标为
的轴相切,和直线AB交于C、D两点(点C的横坐标小于点D的横坐标),设P点的横坐标为 ,试用含有
,试用含有 的代数式表示C点的横坐标;
的代数式表示C点的横坐标;
(3)在(2)的条件下,若点C在线段AB上,求 为何值时,△BOC为等腰三角形.
为何值时,△BOC为等腰三角形.
23.(本题满分9分)
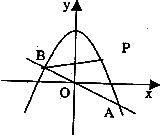
如图,已知直线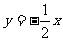 与抛物线
与抛物线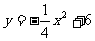 交于A、B两点.
交于A、B两点.
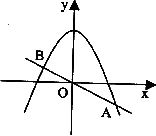
(1)求A、B两点的坐标;
(2)求线段AB的垂直平分线的解析式;
(3)如图,取与线段AB等长的一根橡皮筋,端点分别固定在A、B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A、B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.
22.(本题满分9分)
某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加l0件.
(1) 求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价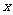 元,商场一天可获利润
元,商场一天可获利润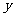 元.
元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出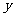 与
与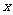 之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当
之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当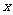 取何值时,商场获利润不少于2160元?
取何值时,商场获利润不少于2160元?
21.(本题满分8分)
一枚均匀的正方体骰子,六个面分别标有数字l,2,3,4,5,6,连续抛掷两次,朝上的数字分别是 ,
,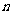 作为点A的横、纵坐标,那么点A(
作为点A的横、纵坐标,那么点A( ,
,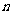 )在函数
)在函数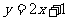 的图像上的概率是多少?
的图像上的概率是多少?
20.(本题满分8分)
(1)解方程: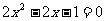
(2)解不等式组
19.(本题满分7分)
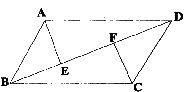
(1)已知:如图,平行四边形ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.
求证:BE=DF.
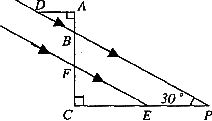
(2)如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为 ,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米。求窗外遮阳蓬外端一点D到窗户上椽的距离AD.(结果精确到0.1米)
,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米。求窗外遮阳蓬外端一点D到窗户上椽的距离AD.(结果精确到0.1米)
18.(本题满分7分)
(1)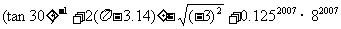
(2)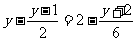
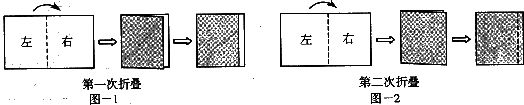
17.小宇同学在一次手工制作活动中,先把一张矩形纸片按图1的方式进行折叠,使折痕的左侧部分比右侧部分短lcm;展开后按图2的方式再折叠一次,使第二次折痕的左侧.部分比右侧部分长lcm,再展开后,在纸上形成的两条折痕之间的距离是________cm
16. 如图,直线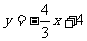 与
与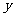 轴交于点A,与直线
轴交于点A,与直线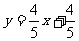 交于点B,且直线
交于点B,且直线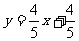 与
与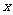 轴交于点C,则△ABC的面积为___________
轴交于点C,则△ABC的面积为___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com