
4.要直观地反映出某种股票的涨跌情况,应选择
(A)条形的统计图 (B)扇形的统计图
(C)折线的统计图 (D)直方图
3.如图,E,B,F,C四点在一条直线上EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是
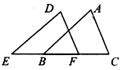
(A)AB =DE (B)DF∥AC (C)∠E=∠ABC (D)AB∥DE
2.函数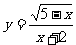 中自变量
中自变量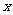 的取值范围是
的取值范围是
(A)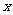 ≥5 (B)
≥5 (B)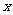 ≤5且
≤5且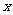 ≠-2
≠-2
(C)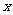 ≤5 (D)
≤5 (D)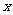 <5上
<5上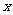 ≠-2
≠-2
1.下列运算中,计算结果正确的是
(A)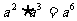 (B)
(B)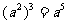
(C)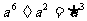 (D)
(D)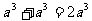
31.已知抛物线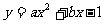 经过点A(一1,0)、B(m,0)(m>0),且与y轴交于点C
经过点A(一1,0)、B(m,0)(m>0),且与y轴交于点C
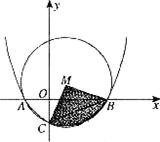
(1)求抛物线对应的函数表达式(用含m的式子表示);
(2)如图,⊙M经过A、B、C三点,求扇形MBC(阴影部分)的面积S(用含m的式子表示);
(3)若抛物线上存在点P,使得△APB∽△ABC,求m的值.
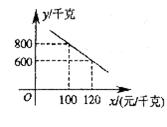
30.某海参养殖公司经市场调研发现,每周该公司销售的海参量y(千克)与单价 (元/千克)之间存在如图所示的一次函数关系.
(元/千克)之间存在如图所示的一次函数关系.
(1)根据图象求y与 之间的函数表达式;
之间的函数表达式;
(2)从经济效益来看,你认为该公司如何制定海参单价,能使每周海参的销售收入最高?每周海参的最高销售收入是多少?
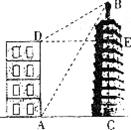
29.如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据: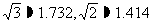 )
)
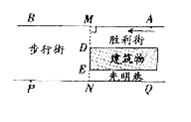
28.如图,一段街道的两边缘所在直线分别为AB、PQ,并且AB//PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线及此时小亮所在位置(用点C标出);
(2)若MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
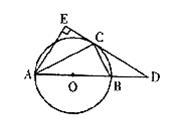
27.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB的延长线上的一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.求证:DE是⊙O的切线.
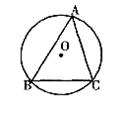
26.如图,⊙O是△ABC的外接圆,∠BAC=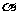 ,弦BC=sin
,弦BC=sin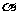 ,试探究⊙O的半径的值.
,试探究⊙O的半径的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com