
4.下列运算正确的是 ( )
A、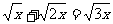 B、
B、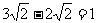
C、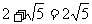 D、
D、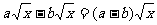
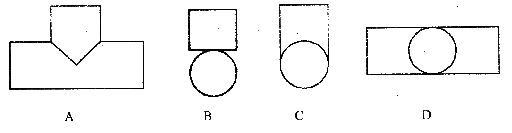
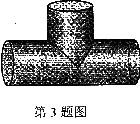
3.如图是一个水管的三叉接头,它的左视图是 ( )
2.平面直角坐标系中,点P(1,4)在 ( )
A、第一象限 B、第二象限
C、第三象限 D、第四象限
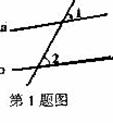
1.如图1,已知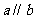 ,
,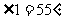 ,则
,则 的大小是 ( )
的大小是 ( )
A、35° B、125° C、145° D、55°
25.在平面直角坐标系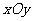 ,已知直线
,已知直线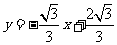 交
交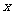 于点C,交
于点C,交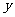 轴于点A。等腰直角三角板OBD的顶点D与点G重合,如图l6一①所示.把三角板绕着点O顺时针旋转,旋转角度为
轴于点A。等腰直角三角板OBD的顶点D与点G重合,如图l6一①所示.把三角板绕着点O顺时针旋转,旋转角度为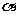 (
(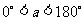 ),使B点恰好落在AC上的
),使B点恰好落在AC上的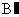 。如图l6一②所示。
。如图l6一②所示。
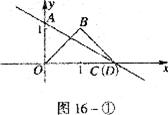
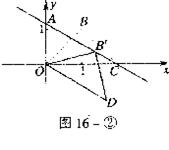
(1)求图l6一①中的点B的坐标;
(2)求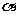 的值;
的值;
(3)若二次函数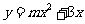 的图像经过(1)中的点B,判断点
的图像经过(1)中的点B,判断点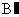 是否在这条抛物线上,并说明理由。
是否在这条抛物线上,并说明理由。
24.已知:点P为线段AB上的动点(与A、B两点不重合)。在同一平面内,把线段AP、BP分别折成 CDP、
CDP、 EFP,其中
EFP,其中 CDP=
CDP= EFP=90°,且D、P、F三点共线。如图15所示。
EFP=90°,且D、P、F三点共线。如图15所示。
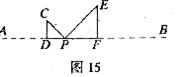
(1)若△CDP、△EFP均为等腰三角形,且DF=2,求AB的长;
(2)若AB=12,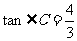 ,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值。
,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值。
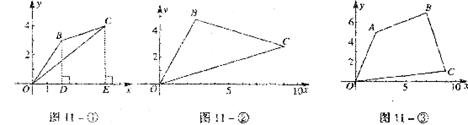
22.例,如图11一①,平面直角坐标系中有点B(2,3)和C(5,4):求△OBC的面积。
解:过点B作BD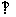
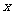 轴于D,过点C作CE
轴于D,过点C作CE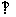
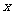 轴于E。依题意,可得
轴于E。依题意,可得
S△OBC=S梯形BDEC+ S△OBD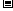 S△OCE
S△OCE
=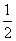 (BD+CE)(OE-OD)+
(BD+CE)(OE-OD)+ 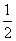 OD
OD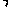 BD
BD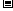
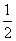 OE
OE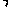 CE
CE
=
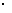 (3+4)
(3+4) 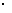 (5-2)+
(5-2)+ 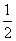
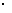 5
5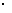 4=3.5
4=3.5
∴ OBC的面积为3.5。
OBC的面积为3.5。
(1)如图11一②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上。仿照例题的解法,求 OBC的面积(用x1,y1、x2,y2的代数式表示);
OBC的面积(用x1,y1、x2,y2的代数式表示);
(2)如图11一③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积。
21.如图10,AB经过⊙O的圆心,弦DF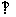 AB于E,BF切⊙O于F,⊙O的半径为2。
AB于E,BF切⊙O于F,⊙O的半径为2。
(1)求证:BD与⊙O相切;
(2)若 ABD=
ABD= DFC,求DF的长。
DFC,求DF的长。
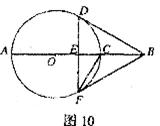
20.某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远。有关数据整理如下:
|
立定跳远成绩(分) |
学生人数(人) |
|
10 |
m |
|
9 |
16 |
|
8 |
4 |
|
7 |
n |
|
6 |
2 |
|
5 |
2 |
|
合计 |
|
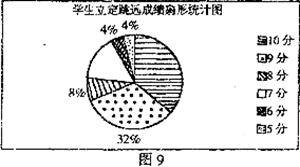
(1)依据图表信息,可知此次调查的样本容量为 ;
(2)在扇形统计图(如图9)中表示立定跳远成绩为8分的扇形圆心角的度数为 。(精确到1°);
(3)已知测试成绩为10分的学生比成绩为7分的学生多10人,求m和n的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com