
19.如图,一次函数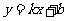 的图象与反比例函数
的图象与反比例函数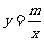 的图象交于
的图象交于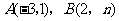 两点,直线
两点,直线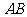 分别交
分别交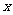 轴、
轴、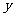 轴于
轴于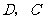 两点.
两点.
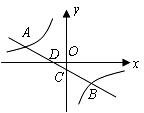
(1)求上述反比例函数和一次函数的解析式;
(2)求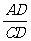 的值.
的值.
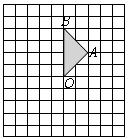
18.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.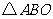 的三个顶点
的三个顶点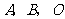 都在格点上.
都在格点上.
(1)画出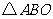 绕点
绕点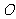 逆时针旋转
逆时针旋转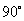 后得到的三角形;
后得到的三角形;
(2)求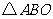 在上述旋转过程中所扫过的面积.
在上述旋转过程中所扫过的面积.
17.(1)计算: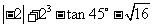
(2)解方程: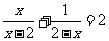
16.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径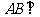 弦
弦 于
于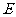 ),设
),设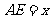 ,
,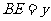 ,他用含
,他用含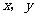 的式子表示图中的弦
的式子表示图中的弦 的长度,通过比较运动的弦
的长度,通过比较运动的弦 和与之垂直的直径
和与之垂直的直径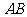 的大小关系,发现了一个关于正数
的大小关系,发现了一个关于正数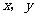 的不等式,你也能发现这个不等式吗?写出你发现的不等式
.
的不等式,你也能发现这个不等式吗?写出你发现的不等式
.
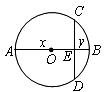
15.如图,四边形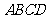 ,
,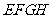 ,
,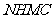 都是正方形,边长分别为
都是正方形,边长分别为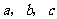 ;
;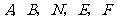 五点在同一直线上,则
五点在同一直线上,则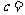 (用含有
(用含有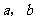 的代数式表示).
的代数式表示).
14.如图,从地面垂直向上抛出一小球,小球的高度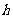 (单位:米)与小球运动时间
(单位:米)与小球运动时间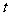 (单位:秒)的函数关系式是
(单位:秒)的函数关系式是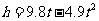 ,那么小球运动中的最大高度
,那么小球运动中的最大高度 .
.
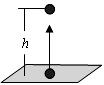
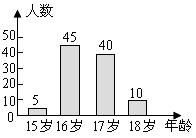
13.台州市某中学随机调查了部分九年级学生的年龄,并画出了这些学生的年龄分布统计图(如图),那么,从该校九年级中任抽一名学生,抽到学生的年龄是16岁的概率是 .
12.因式分解: .
.
11.化简: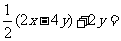 .
.
10.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
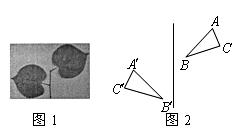
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com