
24.(本小题12分)
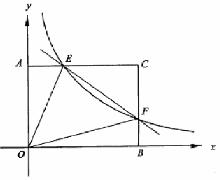
已知:在矩形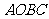 中,
中,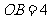 ,
,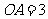 .分别以
.分别以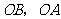 所在直线为
所在直线为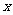 轴和
轴和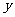 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.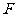 是边
是边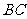 上的一个动点(不与
上的一个动点(不与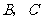 重合),过
重合),过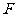 点的反比例函数
点的反比例函数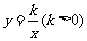 的图象与
的图象与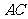 边交于点
边交于点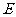 .
.
(1)求证: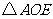 与
与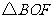 的面积相等;
的面积相等;
(2)记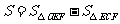 ,求当
,求当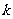 为何值时,
为何值时,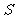 有最大值,最大值为多少?
有最大值,最大值为多少?
(3)请探索:是否存在这样的点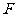 ,使得将
,使得将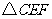 沿
沿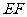 对折后,
对折后,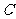 点恰好落在
点恰好落在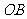 上?若存在,求出点
上?若存在,求出点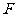 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
23.(本小题10分)
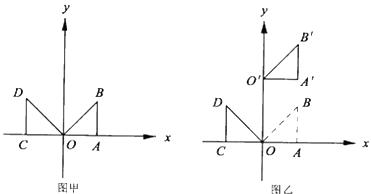
如图甲,在等腰直角三角形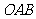 中,
中,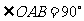 ,
,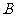 点在第一象限,
点在第一象限,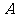 点坐标为
点坐标为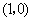 ,
,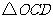 与
与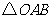 关于
关于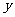 轴对称.
轴对称.
(1)求经过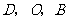 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)若将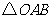 向上平移
向上平移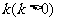 个单位至
个单位至 (如图乙),则经过
(如图乙),则经过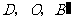 三点的抛物线的对称轴在
三点的抛物线的对称轴在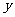 轴的 .(填“左侧”或“右侧”)
轴的 .(填“左侧”或“右侧”)
(3)在(2)的条件下,设过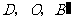 三点的抛物线的对称轴为直线
三点的抛物线的对称轴为直线 .求当
.求当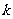 为何值时,
为何值时,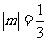 ?
?
22.(本小题10分)
为了支援四川人民抗震救灾,某休闲用品有限公司主动承担了为灾区生产2万顶帐篷的任务,计划10天完成.
(1)按此计划,该公司平均每天应生产帐篷 顶;
(2)生产2天后,公司又从其它部门抽调了50名工人参加帐篷生产,同时,通过技术革新等手段使每位工人的工作效率比原计划提高了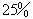 ,结果提前2天完成了生产任务.求该公司原计划安排多少名工人生产帐篷?
,结果提前2天完成了生产任务.求该公司原计划安排多少名工人生产帐篷?
20.(本小题8分)
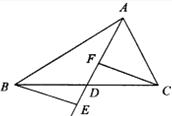
如图,在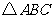 中,
中,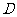 是
是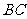 边的中点,
边的中点,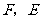 分别是
分别是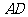 及其延长线上的点,
及其延长线上的点,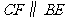 .
.
(1)求证: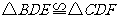 .
.
(2)请连结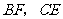 ,试判断四边形
,试判断四边形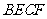 是何种特殊四边形,并说明理由.
是何种特殊四边形,并说明理由.
19.(本题有2小题,每小题5分,共10分)
(1)计算: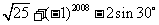 ;
;
(2)解不等式组: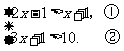
18.将自然数按以下规律排列,则2008所在的位置是第 行第 列.

17.一个长、宽、高分别为15cm,10cm,5cm的长方体包装盒的表面积为 cm2.
16.如图, 是⊙
是⊙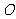 的直径,
的直径,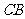 切⊙
切⊙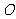 于
于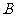 ,连结
,连结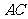 交⊙
交⊙ 于
于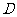 ,若
,若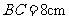 ,
,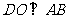 ,则⊙
,则⊙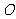 的半径
的半径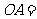 cm.
cm.
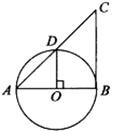
15.利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为 ,该定理的结论其数学表达式是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com