
7.若|x+3|+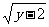 =0,则x+2y的值为( )
=0,则x+2y的值为( )
A.0 B.-1 C.1 D.5
6.将抛物线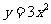 向上平移2个单位,得到抛物线的解析式是
向上平移2个单位,得到抛物线的解析式是
A.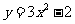 B.
B.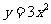 C.
C.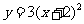 D.
D.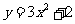
5.把中考体检调查学生的身高作为样本,样本数据落在1.6-2.0(单位:米)之间的频率为0.28,于是可估计2 000名体检中学生中,身高在1.6-2.0米之间的学生有
A.56 B.560 C.80 D.150
4.在Rt△ABC中,∠C = 90°,若BC = 2AC,则tanA的值是
A.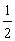 B.2 C.
B.2 C.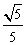 D.
D.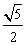
3.下列长度的三条线段,能组成三角形的是
A.1 cm,2 cm,3 cm B.2 cm,3 cm,6 cm
C.4 cm,6 cm,8 cm D.5 cm,6 cm,12 cm
2.化简(-a2)3 的结果
A.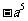 B.
B.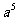 C.
C.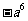 D.
D.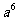
1.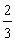 的相反数是
的相反数是
A.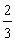 B.-
B.-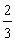 C.
C.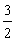 D.-
D.-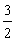
25.(本小题8分)
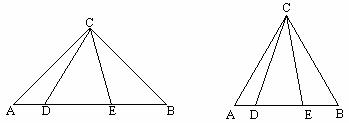
图① 图②
(1) 已知:如图①,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上,且∠DCE=45°. 求证:线段DE、AD、EB总能构成一个直角三角形;
(2)已知:如图②,等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数;
(3)在(1)的条件下,如果AB=10,求BD·AE的值.
24.(本小题7分)
抛物线与x轴交于A(-1,0)、B两点,与y轴交于点C(0,-3),抛物线顶点为M,连接AC并延长AC交抛物线对称轴于点Q,且点Q到x轴的距离为6.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,求出点D的坐标;
(3)抛物线对称轴上是否存在一点P,使得S△PAM=3S△ACM,若存在,求出P点坐标;若不存在,请说明理由.
23.(本小题5分)
将图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,
△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
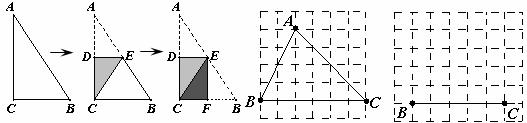
图① 图② 图③
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com