
解:令x=1,则有(-1)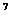 =a
=a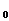 +a
+a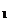 +a
+a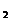 +…+a
+…+a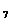 =-1;令x=0,则有a
=-1;令x=0,则有a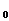 =1。所以a
=1。所以a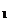 +a
+a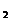 +…+a
+…+a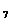 =-1-1=-2。
=-1-1=-2。
分析:题目中“求值”二字提供了这样信息:答案为一定值,于是不妨令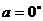 ,得结果为
,得结果为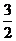 。已知(1-2x)
。已知(1-2x)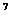 =a
=a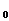 +a
+a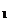 x+a
x+a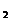 x
x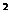 +…+a
+…+a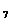 x
x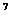 ,那么a
,那么a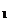 +a
+a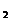 +…+a
+…+a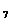 = 。
= 。
例14、 求值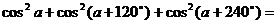 。
。
设k = 0,因抛物线焦点坐标为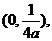 把直线方程
把直线方程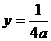 代入抛物线方程得
代入抛物线方程得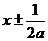 ,∴
,∴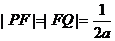 ,从而
,从而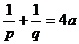 。
。
例13、 过抛物线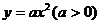 的焦点F作一直线交抛物线交于P、Q两点,若线段PF、FQ的长分别为p、q,则
的焦点F作一直线交抛物线交于P、Q两点,若线段PF、FQ的长分别为p、q,则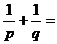 。
。
解:此抛物线开口向上,过焦点且斜率为k的直线与抛物线均有两个交点P、Q,当k变化时PF、FQ的长均变化,但从题设可以得到这样的信息:尽管PF、FQ不定,但其倒数和应为定值,所以可以针对直线的某一特定位置进行求解,而不失一般性。
解:特殊化:令 ,则△ABC为直角三角形,
,则△ABC为直角三角形,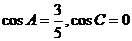 ,从而所求值为
,从而所求值为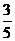 。
。
例12、在△ABC中,角A、B、C所对的边分别为a、b、c。若a、b、c成等差数列,则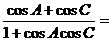 。
。
例11、已知(1-2x)7=a0+a1x+a2x2+…+a7x7,那么a1+a2+…+a7=_____.
解:将已知与求解对照:
a0+a1x+a2x2+…+a7x7=(1-2x)7,
a1+a2+…+a7=?
可见取x=0时,得a0=1;再取x=1以求值.有
a1+a2+…+a7=(1-2)7-a0=-2.
说明:通过对未知变量x赋以特殊值0和1,十分简洁地求出了问题的答案,收到了事半功倍的效果.
∴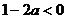 ,∴
,∴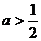 .
.
2、特殊化法:当填空题已知条件中含有某些不确定的量,但填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可以将题中变化的不定量选取一些符合条件的恰当特殊值(或特殊函数,或特殊角,特殊数列,图形特殊位置,特殊点,特殊方程,特殊模型等)进行处理,从而得出探求的结论.这样可大大地简化推理、论证的过程.
解: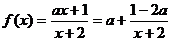 ,由复合函数的增减性可知,
,由复合函数的增减性可知, 在
在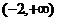 上为增函数,
上为增函数,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com