
11. 倒数:乘积得1的两个数互为倒数。即:若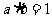 ,则a与b互为倒数。
,则a与b互为倒数。
且反之也成立:即a与b互为倒数,则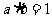
提示:
(1)零没有倒数。
(2)互为倒数的两个数的符号相同。
如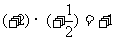
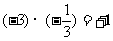
(3)要与相反数区别开:相加为0的两个数互为相反数。即:a+b=0,则a与b互为相反数,且反之也成立。
[典型例题]
例1:1)(-3)-(-4)
解:原式=-3+4 减去一个数等于加上它的相反数
=+1 取绝对值较大的数的符号并用较大的绝对值减去较小的绝对值
2)(+16)-(+27)+(-5)-(-42)
解:原式=(+16)+(-27)+(-5)+(+42)(统一为加法)
=+16-27-5+42 (省略加号的代数和)
=+16+42-27-5(用交换律化简)=58-32=26
例2:已知a>0,b<0,试判断a-b的符号
分析:由b<0得-b>0,再进行a-b的运算
解: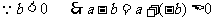
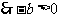 正+正
正+正
例3: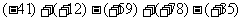 加减混合统一成加法
加减混合统一成加法
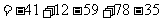 省略加号形式
省略加号形式
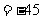 正数结合、负数结合简化计算
正数结合、负数结合简化计算
例4:1998+89-95-997
解法一:
原式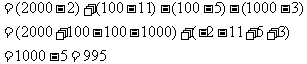
解法二:原式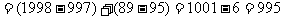
例5:
解:原式=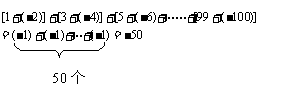
例6:求数轴上表示+2与-8的两点间的距离
分析:求数轴上两点间的距离就是求这两点所表示的有理数之差的绝对值
解: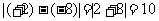
注意:数轴上表示有理数a,b两点间的距离可用|a-b|来求。
例7:选择题
(1)如果两数的和是负数,那么一定不可能的是( )
A. 这两个数都是负数
B. 这两个一个是负数,一个是零
C. 这两个数中一个是正数,另一个是负数,且负数的绝对值较大
D. 这两个数都是正数
(2)对于有理数a,b有下面说法:
<1>若a+b=0,则a与b是互为相反数的数;
<2>若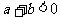 ,则a与b异号;
,则a与b异号;
<3>若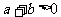 ,且a与b同号,则a>0,b>0;
,且a与b同号,则a>0,b>0;
<4>若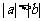 ,且a,b异号,则
,且a,b异号,则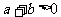 ;
;
<5>若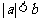 ,则
,则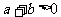 ;其中,正确的说法有( )
;其中,正确的说法有( )
A. 4个 B. 3个 C. 2个 D. 1个
(3)一个数是11,另一个数比11的相反数大2,那么这两个数的和是( )
A. 2 B. -2 C. 24 D. -24
(4)如果一个整数减去-6是正数,减去-4是负数,则这个数减去9等于( )
A. -4 B. 4 C. -14 D. 14
答案:(1)D(2)B(3)A(4)C
例8:数轴上有两个数a、b,如图
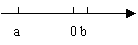
用>把a,b,-a,-b,a+b,a-b连接起来
解: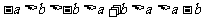 (提示:可以用特殊值法)
(提示:可以用特殊值法)
例9:判断下列积的符号
(1)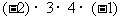
(2)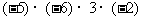
(3)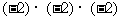
(4)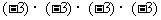
答案:(1)+号(2)-号(3)-号(4)+号
例10:(1)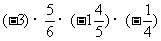
(2)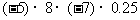
(3)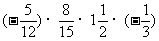
(4)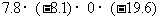
(5)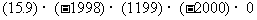
答案:(1)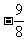 (2)70(3)
(2)70(3)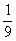 (4)0(5)0
(4)0(5)0
例11:解答下列各题:
(1)某冷库温度是零下10℃,下降-3℃后又下降5℃,两次变化后冷库的温度是多少?
分析:理解题意“下降”“低多少”是要做减法运算
解:(-10)-(-3)-5=(-10)+3-5=-12℃
(2)零下12℃比零上12℃低多少度?
解:12-(-12)=12+12=24℃
例12:计算:
(1)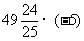
解:原式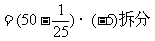
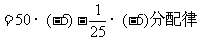
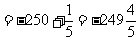
(2)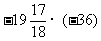
解法1:原式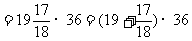
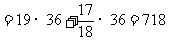
解法2:原式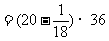
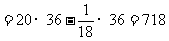
例13:计算:-3.14×35.2+6.28×(-23.3)-1.57×36.4
分析:直接看好像没有什么简算方法,但仔细观察1.57、3.14与6.28之间有倍数关系,可逆用乘法分配律进行计算
解:原式=-3.14×35.2+(-3.14)×46.6+(-3.14)×18.2
=-31.4×(35.2+46.6+18.2)
=-3.14×100=-314
[模拟试题](答题时间:30分钟)
10. 计算乘法时注意以下问题:
(1)当因数是带分数时,应先化成假分数便于约分
(2)第一个因数是负数时,可以不加括号,但后面的负因数必须加括号
(3)若几个有理数相乘时,有一个因数为0,则结果为0
(4)尽量运用运算律,使计算简便准确
9. 计算有理数乘法的步骤:(1)根据符号法则,先确定积的符号
(2)确定积的绝对值
8. 乘法交换律:两个数相乘,交换因数的位置,积不变。
即: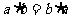
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变
即: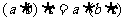
乘法分配律:一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加。
即: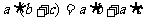 ,有时也可以逆用:
,有时也可以逆用: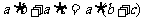
7. 有理数乘法法则的推广:多个不等于0的有理数相乘时,积的符号由负因数的个数决定,当负因数的个数为奇数时,积为负;当负因数的个数为偶数时,积为正。多个有理数相乘时只要有一个是0,积为0。
6. 有理数乘法:两个不为零的有理数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘,都得零。
5. 加减混合运算的方法和步骤:(1)将减法统一成加法,并写成省略加号的形式
(2)运用加法的交换律和结合律,简化运算
(3)计算出结果
技巧:(1)把互为相反数的两个数先加
(2)几个数相加的结果是整数时可以先加
(3)同分母分数先加
(4)正数与正数、负数与负数分别先加
4. 数轴上A、B两点间的距离的求法:
两点间的距离实际就是它们表示的数a,b差的绝对值即: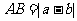
3. 计算减法的步骤:(1)将减号变为加号,同时减数变成原来的相反数(2)按照加法法则进行计算
2. 有理数减法法则:减去一个数等于加上这个数的相反数 即:a-b=a+(-b)
把减法运算转化为加法运算,体现了数学的转化思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com