2、探求验证

　　　 计算下列各题，并比较它们的结果。

　　　 第一组　　　　　　　　　　　　　　　　　　

　　　　 (1)、(-7 )× 8 =　　　　　　　　　　　　

　　　　　　　 8 ×(-7 )= ___________

　　　　 (2)、[(-4-)×(-6)]×5＝____________

　(-4-)×[ (-6)×5]＝____________

(3)、(－2)×[(－3)+()]＝____________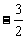

(－2)×(－3)+(-2)()＝________________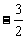

第二组

(1)、()×()＝_______________

()×()＝_______________

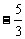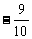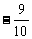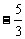(2)、[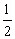×(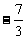)]×(－4)＝_____________

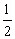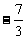×[()]×(－4)]＝_____________

(3)、5×[(-7)+( )]=__________________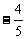

5×(-7)+5×( )]=______________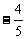

　 让学生自由选择其中的一组问题进行计算，然后在组内交流，验证答案的正确性。

1、复习引入

　　 (1)、 在小学我们学过一些乘法的交换律、乘法的结合律以及分配律，谁能给大家介绍一下？

　　 (2)、小学学习过的有关乘法的运算律，对所有的有理数都还适用吗？

2、教学难点：正确运用运算律，使运算简化。

1、教学重点：用运算律简化运算。

3、　 培养学生语言表达能力以及与他人沟通、交往能力，使其逐渐热爱数学这门课程。

2、　 让学生通过观察、思考、探究、讨论，主动地学习。

1、　 进一步熟悉有理数的乘法运算并能用乘法运算律简化运算。

学生能较顺利地完成学习任务，同时意识到确实应把时间放心地放给学生，充分调动学生的积极性、主动性。本节不足之处是：仍有学生不按一确定符号，二确定积绝对值来运用法则，故而符号上仍有错误之处。

2、　 难点：概括总结乘法法则及运算中的符号问题。