
3.下列函数中,y是x的正比例函数的是( )
A.y=2x-1 B.y=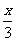 C.y=2x2 D.y=-2x+1
C.y=2x2 D.y=-2x+1
2.下面哪个点在函数y=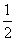 x+1的图象上( )
x+1的图象上( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
1.下列函数中,自变量x的取值范围是x≥2的是( )
A.y=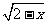 B.y=
B.y=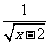 C.y=
C.y= D.y=
D.y=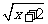 ·
·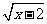
复习旧知--情景设置、获得新知--数形结合(画图象)、另获新知--学习范例、应用所学--随堂练习、期待提高--课堂小结、形成认识--布置作业、提高认识
教学过程设计
[活动1]复习旧知
经过上节课的学习,请同学们帮助老师出一些问题考考咱们班的同学,好吗?
教师行为:放手让学生活动,只是在学生回答的过程中及时纠正出现的问题。
学生行为:学生思考后积极出题,并回答其他同学的问题。
本次活动重点关注:(1)学生在活动中的参与意识、出问题和回答问题的勇气。(2)学生在出题和答题过程中知识掌握怎么样,语言表达是否规范。
[活动2]情景设置、获得新知
问题(投影展示)1、某登山队大本营所在地的气温为5摄氏度,海拔每升高1千米,气温下降6摄氏度,登山队员由大本营向上登高x(千米时),他们所在位置的气温是y(摄氏度),试用解析式表示y与x的关系。
下列问题中变量间的对应关系可用怎样的函数表示?这些函数有什么共同点?
有人发现,在20-25摄氏度时蟋蟀每分鸣叫次数C与温度(摄氏度)有关,即C的值约是t的7倍与35的差。
某城市市内电话的月收费额y(元)包括:月租费15元,拨打电话x分的计时费按0.01元/分收取。
把一个长10厘米,宽5厘米的长方形的长减少x,宽不变,长方形的面积y(平方厘米)随x的变化而变化。
学生活动:1、活动形式:学生可以独立思考,可以分组讨论。2、寻找解题途径,列出关系式。3、比较归纳,争取得到结论。
教师行为:1、课堂调控,防止意外事情的发生。2、及时发现学生活动中出现的问题,做好个别辅导,引导其完成本次活动。
师生达成共识:1、教师把问题1、2中所涉及的关系式在黑板上“有目的”、准确的表示出来。2、让学生回答得出的结论,而后形成共识,得出一次函数的概念:一般地,如果变量y与变量x有关系式y=kx+b(k、b是常数,且k≠0),那么,y叫做x的一次函数.
解析式:y=kx+b(k≠0)
本次活动中重点关注:1、学生探索的参与热情。2、学生获得新知的情况。3、学生学习一次函数时,概念的语言表述是否准确、流畅,表达一般形式时,是否注意k≠0的重要条件。
[活动3]数形结合(画图象)、另获新知
问题:画函数y=2x+3和y=-2x-2的图象。
学生活动:1、按照画函数图象的步骤,独立画出上面两个一次函数的图象,并找一个学生在黑板上画图。2、图象画完之后,注意观察两个函数图象的特征,进行总结。3、探究过程中可与其他同学进行讨论。
教师行为:1、关注全体学生,做好个别辅导,指导其完成上述任务。2、引导学生归纳得出一般性结论。
师生形成共识:1、一次函数图象的形状是一条直线。2、截距。3、感悟:因为只需两点就可以确定一条直线,因此作一次函数的图象实际上只要在直角坐标系里的直线上任取两点,然后过这两点画一条直线就行了。
本次活动重点关注:1、学生的动手操作能力。2、学生的归纳能力。3、由于画函数图象是一个复杂的工程,在活动中要关注学生的意志品质。
[活动4]学习范例、应用所学
问题:画直线y=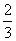 x-2的图象。
x-2的图象。
学生活动:画图,尽量取最简单的点,然后连线。
教师行为:对画图思路进行点拨,并安排学生上台板演。
师生形成共识:画一次函数图象的最简单方法就是取简单地点,如(0,b),(-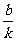 ,0)。
,0)。
本次活动重点关注:学生能否准确的画出图象,能不能用最简单的办法画出图象。
[活动5]随堂练习、期待提高
问题:课本第38页练习。
学生活动:动手画出四个图形,并小结画图方法。
教师行为:面向全体学生,做好个别辅导。
师生形成共识:画一次函数图象的方法:(1)取点:尽量简单的点;(2)建立直角坐标系,描出两点;(3)连接。
本次活动重点关注:学生能否熟练的画出一次函数的图象,掌握一次函数图象的画法。
[活动6]课堂小结、形成认识
问题:1、本节课我们学了哪些方面的知识?
通过本节课的学习你有哪些体会?
学生活动:积极思考,认真总结。
教师行为:引导学生回忆本节课所学过的知识。
师生形成共识:1、一次函数的一般表达式y=kx+b(k≠0)及截距。
一次函数的图象是一条直线。
一次函数图象的画法:(1)取点:尽量简单的点;(2)建立直角坐标系,描出两点;(3)连接。
本次活动重点关注:1、学生归纳总结能力。2、语言表达能力。3、对一次函数条件的关注。
布置作业、提高认识
课本第44页习题13.2第1、2两题。(必做题)
如果你有能力,请画出y=5x、y=5x+2、y=5x-3的图象,并能说出后两个图象是第一个图像怎样平移得到的吗?(选做题)
本次活动重点关注:分层次布置作业,让不同能力的学生都得到锻炼。
教学反思:
2、难点:领会一次函数的概念,培养抽象思维。
1、重点:理解一次函数概念,会画一次函数图象。
3、情感、态度与价值观
培养抽象思维,发展数形结合的思想,体会一次函数的应用价值。
2、过程与方法
经历探索一次函数的过程,发展学生的抽象思维能力。
1、知识与技能
理解一次函数的概念、图象,明确一次函数的图象是一条直线。
4、教具准备:多媒体工具。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com