1、　 圆柱的底面半径是10㎝。①当圆柱的高由小变大时圆柱的体积___________；②在这个变化 过程中，自变量是_________，因变量是_________；③若圆柱的高为h，则圆柱的体积V=_______；④当高由1㎝变化到10㎝时，圆柱的体积由__________㎝³变化到___________㎝³；⑤当h=0时，V=__________，此时它表示的是____________。

4．小结

　　 问题一　 如何用树状图列出所有可能的结果(基本事件)?举例说明；

　　 问题二　 如何用表格列出所有可能的结果(基本事件)?举例说明．

3．例题教学

　　 课本安排了两个例题，应鼓励学生先尝试、思考，再研究讨论和计算．　

2．探索活动

　　 根据课本中列举的活动进行探索交流．除课本提供的素材外，教师还可选择一些更能引起学生兴趣和思考的探索问题．

　　 例如，一辆汽车向东行驶(如图)．当汽车驶到十字路口时，它可以自由选择向左或向右或向前行驶，当通过第二个十字路口后，求下列事件发生的概率：

　　 (1)汽车向东行驶，

　　 (2)汽车向北行驶，

　　 (3)汽车向西或向北行驶，

(4)汽车不向南行驶．

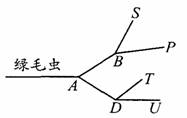　　 又如，如图，一个树叉，一绿毛虫要去吃树叶．如果绿毛虫选择叉枝是等可能的，求下列事件发生的概率：

　　 (1)绿毛虫吃到树叶S；

　　 (2)绿毛虫吃到树叶了；

(3)绿毛虫吃到树叶B．

1．情境创设

　　 课本提供的情境是掷一枚硬币2次，可以继续追问“掷一枚硬币3次都是正面朝上的概率是多少?”．除课本提供的试验素材外，还可以创设更能引起学生兴趣和思考的游戏活动情境．例如，两人掷一枚均匀的骰子，一人一次．在做游戏之前，每人说一个数，如果抛掷的骰子两次朝上的点数之和恰与某人的一样，那么该人获胜．要想取得胜利，你会说哪个数?让学生切实感受到，树状图和列表格既形象又直观，可以帮助我们既不重复也不遗漏地列出所有可能的结果(基本事件)，从而计算古典概型中事件所含的可能结果(基本事件)数及事件发生的概率．

4．小结

　　 问题一　 等可能条件下的概率(一)即古典概型的两个基本特征是什么?

　　 问题二　 如何计算等可能条件下的概率(一)即古典概型中事件的概率?

[教学过程(第二课时)]

3．例题教学

　　 课本安排了两个例题，应鼓励学生先尝试、思考，再研究讨论和计算．

2．探索活动

　　 根据课本中列举的活动进行探索交流．教学时要注意突出等可能条件下的概率(一)(即古典概型)的两个基本特征--试验结果的有限性和等可能性．并不是所有的试验都是古典概型，一个试验是否为古典概型，关键在于这个试验是否具备古典概型的两个特征．例如，一射手射击打靶，“中靶”与“脱靶”一般不是等可能的．又如，从规格直径为100mm±0.2mm的一批合格产品中任意抽测1件，其直径可能是从99.8mm到100.2mm之间的任何一个值，所有可能的结果有无穷多个．这两个试验都不是古典概型．根　 据教学的实际情况，可结合上面提供的素材提出问题供学生思考交流，从而进一步丰富对等可能条件下的概率(一)(即古典概型)的认识．

1．情境创设

　　 课本创设的问题情境，采用了从特殊到一般的思路：提出问题一思考交流一抽象概括一等可能条件下的概率(一)(即古典概型)．教学时，可多举几个随机试验，例如，掷一枚均匀的硬币、摸球、抽签等，通过分析，再抽象概括出等可能条件下的概率(一)(即古典概型)．

4．会用列举法(包括列表、画树状图)计算一些随机事件所含的可能结果(基本事件)数及事件发生的概率．

[教学过程(第一课时)]