2．根据三角形面积公式可知：

　　 当高h为1cm时，面积S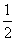＝×5×1=2．5cm²

　　 当高h为2cm时，面积S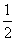＝×5×2=5cm²

　　 …　　 …

　　 当高为hcm，面积S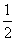＝×5×h=2．5hcm²

　　 其中底边长为5cm是常量，面积S与高h是变量．

　　 Ⅳ．课时小结

　　 本节课从现实问题出发，找出了寻求事物变化中变量之间变化规律的一般方法步骤．它对以后学习函数及建立函数关系式有很重要意义．

2．一个三角形的底边长5cm，高h可以任意伸缩．写出面积S随h变化关系式，并指出其中常量与变量．

　　 解：1．买1支铅笔价值　 1×0．2=0．2(元)

　　 买2支铅笔价值　 2×0．2=0．4(元)

　　 ……

　　 买x支铅笔价值　 x×0．2=0．2x(元)

　　 所以　 y=0．2x

　　 其中单价0．2元／支是常量，总价y元与支数x是变量．

1．购买一些铅笔，单价0．2元／支，总价y元随铅笔支数x变化，指出其中的常量与变量，并写出关系式．

2．因矩形两组对边相等，所以它一条长与一条宽的和应是周长10cm的一半，即5cm．

　　 若长为1cm，则宽为5-1=4(cm)

　　 据矩形面积公式：S＝1×4=4(cm²)

　　 若长为2cm，则宽为5-2=3(cm)

　　 面积　 S＝2×(5-2)=6(cm²)

　　 …　　 …

　　 若长为xcm，则宽为5-x(cm)

　　 面积　 S=x·(5-x)=5x-x²(cm²)

　　 从以上两个题中可以看出，在探索变量间变化规律时，可利用以前学过的一些有关知识公式进行分析寻找，以便尽快找出之间关系，确定关系式．

　　 Ⅲ．随堂练习

1．要求已知面积的圆的半径，可利用圆的面积公式经过变形求出S=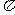r² r=

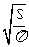
　　 面积为10cm²的圆半径r=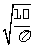≈1．78(cm)

　　 面积为20cm²的圆半径r=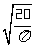≈2．52(cm)

　　 关系式：r＝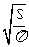

2．用10m长的绳子围成矩形，试改变矩形长度．观察矩形的面积怎样变化．记录不同的矩形的长度值，计算相应的矩形面积的值，探索它们的变化规律：设矩形的长度为xcm，面积为Scm²．怎样用含有x的式子表示S？

结论：

1．要画一个面积为10cm²的圆，圆的半径应取多少？圆的面积为20cm²呢？怎样用含有圆面积S的式子表示圆半径r？

2．挂1kg重物时弹簧长度： 1×0．5+10=10．5(cm)

　　 挂2kg重物时弹簧长度：2×0．5+10=11(cm)

　　 挂3kg重物时弹簧长度：3×0．5+10=11．5(cm)

　　 关系式：L=0．5m+10

　　 通过上述活动，我们清楚地认识到，要想寻求事物变化过程的规律，首先需确定在这个过程中哪些量是变化的，而哪些量又是不变的．在一个变化过程中，我们称数值发生变化的量为变量(variable)，那么数值始终不变的量称之为常量(constant)．如上述两个过程中，售出票数x、票房收入y；重物质量m，弹簧长度L都是变量．而票价10元，弹簧原长10cm……都是常量．

　 [活动二]

1．早场电影票房收入：150×10=1500(元)

　　 日场电影票房收入：205×10=2050(元)

　　 晚场电影票房收入：310×10=3100(元)

　　 关系式：y=10x

2．在一根弹簧的下端悬挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律．如果弹簧原长10cm，每1kg重物使弹簧伸长0．5cm，怎样用含有重物质量m的式子表示受力后的弹簧长度？

　　 引导学生通过合理、正确的思维方法探索出变化规律．

　结论：