
1.理解一次函数与二元一次方程(组)的关系。
6、某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元,厂方在开展促销活动期间向客户提供两种优惠方案:
方案一、买一套西装送一条领带
方案二、西装和领带均按定价的90%付款
某商店老板现要到该服装厂购买西装20套,领带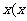 >20)条,请你根据
>20)条,请你根据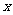 的不同情况,帮助商店老板选择最省钱的购买方案。
的不同情况,帮助商店老板选择最省钱的购买方案。
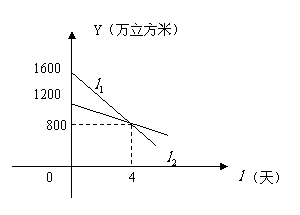
5、如图: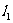 、
、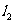 分别表示甲、乙两座水库蓄水量
分别表示甲、乙两座水库蓄水量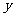 (万立方米)与放水时间t(天)之间的关系
(万立方米)与放水时间t(天)之间的关系
(1)甲水库原来库存多少万立方米?
(2)乙水库平均每天放水多少万立方米?
(3)分别写出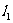 、
、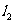 中
中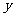 与t的关系式
与t的关系式
(4)经过多少天,乙水库剩水是甲水库剩水的2倍?

4、在直角坐标第中,直线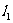 经过点(2,3)和(-1,-3),直线
经过点(2,3)和(-1,-3),直线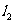 经过原点且与直线
经过原点且与直线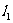 交于(-2,
交于(-2,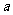 )
)
(1)试求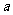 的值
的值
(2)试问(-2,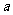 )可看作是怎样的二元一次方程组的解?
)可看作是怎样的二元一次方程组的解?
(3)设交点坐标为P,直线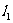 与
与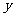 轴交于点A,你能求出△APO的面积吗?不妨试试看。
轴交于点A,你能求出△APO的面积吗?不妨试试看。
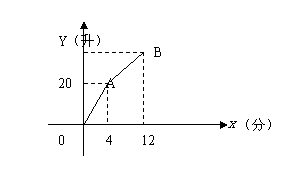
3、一个有进水管与出水管的容器,单位时间内进出的水量都是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,容器内的水量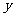 (单位:升)与时间
(单位:升)与时间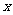 (单位:分)之间的关系如图:
(单位:分)之间的关系如图:
(1)求0≤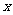 ≤4时,
≤4时,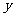 随
随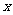 变化的函数关系式
变化的函数关系式
(2)求4≤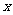 ≤12时,
≤12时,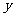 随
随 变化的函数关系式
变化的函数关系式
(3)每分钟进水,出水各为多少升?


2、用图象法解不等式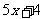 <
<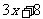
1、已知:一次函数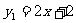 和
和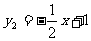 ,画函数图象回答下列问题
,画函数图象回答下列问题
(1)求方程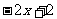 =0的解
=0的解
(2)求不等式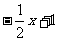 <0的解集
<0的解集
(3)求方程组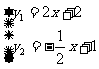 的解
的解
(4)当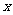 为何值时,
为何值时,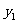 <
<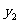
(5)当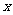 为何值时,
为何值时,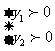
(6)当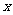 为何值时,
为何值时,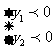
(7)在-1≤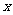 ≤2范围内,求
≤2范围内,求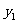 和
和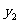 的最大值和最小值
的最大值和最小值
3、一次函数与二元一次方程
求两直线的交点,可通过解方程组,解方程组可通过画图,两直线的交点坐标即为方程组的解
2、一次函数与一元一次不等式的关系:
任何一元一次不等式都可以转化为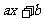 >0或
>0或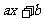 <0(
<0(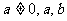 为常数)的形式,所以解一元一次不等式可看作:当一次函数值得大(小)0时,求自变量的取值范围
为常数)的形式,所以解一元一次不等式可看作:当一次函数值得大(小)0时,求自变量的取值范围
1、一次函数与一元一次方程的关系:
任何一元一次方程都可以转化为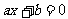 (
(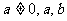 为常数)的形式,所以解一元一次方程是可以转化的,当某个一次函数的值为0时,求相应的自变量的值
为常数)的形式,所以解一元一次方程是可以转化的,当某个一次函数的值为0时,求相应的自变量的值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com