
4、情感态度
(1)通过参与同类项、合并同类项法则的数学探究活动,提高对数学学习的好奇心与求知欲。
(2)在小组活动中体会合作于交流的重要性。
3、解决问题
(1)在经历从具体问题抽象出同类项、合并同类项法则的过程中,发展抽象概括能力。
(2)通过化简列式问题引出同类项概念,发展学生探究能力。
2、数学思考
(1)探索用整式表示事物之间的数量关系,进一步建立符号感,发展抽象思维能力。
(2)通过类比数的运算律得出合并同类项的法则,发展类比的数学思想方法。
1、知识与技能
(1)在具体情景中认识同类项,理解同类项的概念,会识别同类项。
(2)掌握合并同类项的法则,能进行合并同类项。
2.养成实事求是的态度及独立思考的习惯。
教学重点:
探索一次函数与二元一次方程(组)的关系
教学难点:
综合运用方程(组)不等式和函数的知识解决实际问题。
教学程序设计:
|
教学环节 |
教学程序 |
设计意图 |
|||||||||
|
创 设 情 境 设 疑 激 思 |
提 出 问 题 |
1.已知2x-y=1,用含x的代数式表示y,则y= 。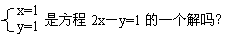 2.方程 2x-y=1的解有 个。 2.方程 2x-y=1的解有 个。3. 4.(1,1)是否是直线y=2x-1上的一个点? |
通过设置问题(1)(2)帮助学生体会到一次函数与二元一次方程的对应关系通过(3)(4)使学生认识到二元一次方程的解与一次函数图象上的点的对应关系。 |
||||||||
|
启 发 提 问 |
1.综合以上几个问题,你能得到哪些启示? |
||||||||||
|
师 生 互 动 探 索 新 知
|
活 动 1 |
1.通过上述问题的讨论,你认为一次函数与二元一次方程有何关系? |
通过问题1。让学生在交流讨论,归纳概括、过程中建立数学模型:一次函数图象上的点与二元一次方程的解间有着对应关系,通过2、3。在进一步理解巩固上而建立起来的模型。问题(4)为活动2打下基础。 |
||||||||
|
2.3x+5y=8对应的一次函数(以x为自变量)是
。 |
|||||||||||
3.直线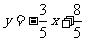 上任取一点(x,y)则(x,y)一定是方程3x+5y=8的解吗?为什么? 上任取一点(x,y)则(x,y)一定是方程3x+5y=8的解吗?为什么? |
|||||||||||
4.在同一直角坐标系中画出直线y=2x-1与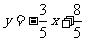 的图象,并思考: 的图象,并思考:(1)它们有交点吗? (2)交点的坐标与方程组 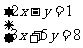 的解有何关系? |
|||||||||||
|
1.由“活动1”中的“问题4”,你能得到哪些启示呢? |
归纳提炼一次函数与二元一次议程组的关系,从“形”的角度理解:解方程组相当于确定两直线交点坐标。 通过2、3使学生从“数”的角度理解:解方程组相当于求自变量为何值时两函数值相等。 |
|||||||||
2.当自变量x取何值时,函数y=2x-1与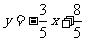 的值相等?这时的函数值是多少? 的值相等?这时的函数值是多少? |
|||||||||||
|
3.问题2与 解方程组 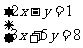 是同一个问题。 是同一个问题。 |
|||||||||||
|
活 动 3 |
1.问题:一家电信公司给顾客提供上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按网时间计费。如何选择收费方式能使上网者更合算。 2.教师活动: 引导学生从实际问题中抽象出具体的数学问题,并应用所学方法求解。 3.学生活动; 在老师引导下,建立两种计费方式的函数模型,然后比较求解。 |
通过活动3,熟悉巩固用一次函数知识求二元一次方程组的问题的方法,进一步提高把实际问题转化为数学问题的能力。 |
|||||||||
|
操 巩 作 固 演 新 练 知 |
下面有两处移动电话计费方式
你知道如何选择计费方式更省钱吗? |
通过本活动让学生进一步理解方程组、不等式与函数之间的联系。 |
|||||||||
|
合 归 作 纳 交 整 流 理 |
学生讨论交流,充分发表自己的意见,共同归纳得到: 1.二元一次方程(组)与一次函数的关系。 2.从“数”和“形”两个方面去看二元一次方程组。 3.方法: 从函数的观点来认识问题、解决问题,图象法解二元一次方程组。 |
通过小结明确本节的主要内容,思想方法,培养学生善于反思和良好习惯。 |
|||||||||
|
课 发 后 散 作 探 业 究 |
课本习题§11·1·3第5、6题和第11题。 |
巩固所学知识,并能解决实际问题。 |
1.积极参与活动,提高学习兴趣及求知欲。
2.体会解决问题的策略多样性发展实践能力和创新精神。
1.体验数形结合思想意义,逐步学习利用数形结合思想分析问题和解决问题,提高解决实际问题的能力。
3.通过学习了解变量问题利用函数方法的优越性。
2.会利用函数图象解二元一次方程组。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com