
3.认知难点与突破方法
难点是能熟练地求出分式有意义的条件,分式的值为零的条件.突破难点的方法是利用分式与分数有许多类似之处,从分数入手,研究出分式的有关概念,同时还要讲清分式与分数的联系与区别.
2.难点:能熟练地求出分式有意义的条件,分式的值为零的条件.
1.重点:理解分式有意义的条件,分式的值为零的条件.
2.理解分式有意义的条件,分式的值为零的条件;能熟练地求出分式有意义的条件,分式的值为零的条件.
1. 了解分式、有理式的概念.
3. 当x为何值时,分式 的值为0?
16.1.1从分数到分式
|
教学目标 |
1. 了解分式、有理式的概念. 2.理解分式有意义的条件,分式的值为零的条件;能熟练地求出分式有意义的条件,分式的值为零的条件. |
|
重点、难点 |
重点:理解分式有意义的条件,分式的值为零的条件. |
|
难点:能熟练地求出分式有意义的条件,分式的值为零的条件. |
|
|
情感态度与价值观 |
熟练地求出分式有意义的条件,分式的值为零的条件.突破难点的方法是利用分式与分数有许多类似之处,从分数入手,研究出分式的有关概念,同时还要讲清分式与分数的联系与区别. |
教 学 过 程
|
教学设计 与 师生互动 |
备 注 |
||
|
第一步:复习提问 1.什么是整式?什么是单项式?什么是多项式? 2.判断下列各式中,哪些是整式?哪些不是整式? ① 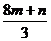 +m2 ②1+x+y2- +m2 ②1+x+y2-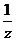 ③ ③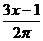 ④ ④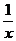 ⑤ 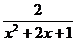 ⑥ ⑥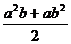 ⑦ ⑦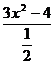 |
|
||
|
第二步:创设情景, P4[思考]让学生自己依次填出: 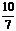 , , , ,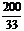 为下面的[观察]提供具体的式 为下面的[观察]提供具体的式子,就以上的式子 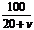 , ,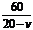 , , , , ,有什么共同点?它们与分数有什么相同点和不同点? ,有什么共同点?它们与分数有什么相同点和不同点?可以发现,这些式子都像分数一样都是 (即A÷B)的形式.分数的分子A与分母B都是整数,而这些式子中的A、B都是整式,并且B中都含有字母. 1.让学生填写P4[思考],学生自己依次填出: 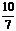 , , , ,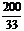 , , . .2.学生看P3的问题:一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用实践,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少? 请同学们跟着教师一起设未知数,列方程. 设江水的流速为x千米/时. 轮船顺流航行100千米所用的时间为 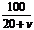 小时,逆流航行60千米所用时间 小时,逆流航行60千米所用时间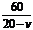 小时,所以 小时,所以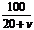 = =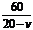 . .3. 以上的式子 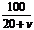 , ,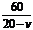 , , , , ,有什么共同点?它们与分数有什么相同点和不同点? ,有什么共同点?它们与分数有什么相同点和不同点? |
|||
|
第三步: 新课讲解: 小结:1.分式的概念:一般地,形如 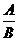 的式子叫做分式,其中A和B均为整式,B中含有字母。 的式子叫做分式,其中A和B均为整式,B中含有字母。练习:下列各式中,哪些是分式哪些不是? (1)、 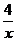 、(2) 、(2)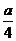 、(3) 、(3)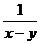 、(4) 、(4)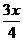 、(5) 、(5)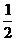 x2、(6) x2、(6)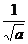 +4 +4强调:(6) 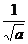 +4带有 +4带有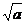 是无理式,不是整式,故不是分式。 是无理式,不是整式,故不是分式。2.小结:对整式、分式的正确区别:分式的分子和分母都是整式,分子可以含有字母,也可以不含有字母,而分母中必须含有字母,这是分式与整式的根本区别。 |
|||
|
第四步:例题讲解 P5例1. 当x为何值时,分式有意义. [分析]已知分式有意义,就可以知道分式的分母不为零,进一步解 出字母x的取值范围. [提问]如果题目为:当x为何值时,分式无意义.你知道怎么解题吗?这样可以使学生一题二用,也可以让学生更全面地感受到分式及有关概念. 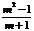 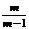 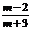 (补充)例2. 当m为何值时,分式的值为0 (补充)例2. 当m为何值时,分式的值为0(1) (2) (3) [分析] 分式的值为0时,必须同时满足两个条件:1分母不能为零;2分子为零,这样求出的m的解集中的公共部分,就是这类题目的解. [答案] (1)m=0 (2)m=2 (3)m=1 |
|||
|
第五步:随堂练习 1.判断下列各式哪些是整式,哪些是分式? 9x+4,  , , 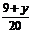 , , 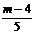 , , 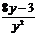 , ,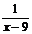 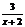 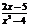 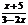 2. 当x取何值时,下列分式有意义? 2. 当x取何值时,下列分式有意义?(1) (2) (3) 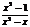 3. 当x为何值时,分式的值为0? 3. 当x为何值时,分式的值为0?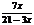 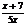 (1) (2)
(3) (1) (2)
(3)
|
|||
|
第六步:课后练习 1.列代数式表示下列数量关系,并指出哪些是正是?哪些是分式? (1)甲每小时做x个零件,则他8小时做零件 个,做80个零件需 小时. (2)轮船在静水中每小时走a千米,水流的速度是b千米/时,轮船的顺流速度是 千米/时,轮船的逆流速度是 千米/时. 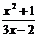 (3)x与y的差于4的商是 . (3)x与y的差于4的商是 .2.当x取何值时,分式 无意义?
课本P51 复习题A组 2、3、4 3、例题与练习 例题1、平行四边形得周长为50cm,两邻边之差为5cm,求各边长。
则AB=_______,BC=________. 变题2.四边形ABCD是平行四边形, ∠BAC=90°,AB=3,AC=4,求AD的长。
变题3.平行四边形ABCD中,AE平分∠DAB, ∠DEA=20°,则∠C=_________, ∠B_______. 变题4.如图,在平行四边形ABCD中, ∠BAC=34°, ∠ACB=26°,求∠DAC与∠D的度数。 例题3.如图,在平行四边形ABCD中,CE⊥AD,CF⊥BA
∠FBC=30°,CE=3cm,CF=5cm, 求平行四边形ABCD的周长。 变题5.如图,平行四边形ABCD的周长为50, 其中AB=15,∠ABC=60°,求平行四边形面积。
2.
同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |