[例1]某校招生录取时，为了防止数据输入出错，2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍，然后让计算机比较两人的输入是否一致.已知甲的输入速度是乙的2倍，结果甲比乙少用2小时输完.问这两个操作员每分钟各能输入多少名学生的成绩？

[分析](1)如何设元(2)题目中有几个相等关系？(3)怎样列方程

解　设乙每分钟能输入x名学生的成绩，则甲每分能输入2x名学生的成绩，根据题意得

＝.

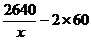解得x＝11.

经检验，x＝11是原方程的解.并且x＝11，2x＝2×11＝22，符合题意.

答：甲每分钟能输入22名学生的成绩，乙每分钟能输入11名学生的成绩.

强调：既要检验所求的解是否是原分式方程的解，还要检验是否符合题意；时间要统一.　 读题、审题、设元、找相等关系列方程.本题有两个相等关系：

(1)甲速=2乙速

(2)甲时+120=乙时

其中(1)用来设，(2)用来列方程

注意如何检验.

2.概　括

列分式方程解应用题的一般步骤：

(1)审清题意；

(2)设未知数(要有单位)；

(3)根据题目中的数量关系列出式子，找出相等关系，列出方程；

(4)解方程，并验根，还要看方程的解是否符合题意；

(5)写出答案(要有单位).

练习：求解本章导图中的问题. 对照题目理解.

2.列方程解应用题的一般步骤？

[概括]这些解题方法与步骤，对于学习分式方程应用题也适用.这节课，我们将学习列分式方程解应用题.　

讨论后回答.

1.复习练习

解下列方程： (1)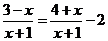　　　 (2)

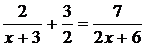
17．3可化为一元一次方程的分式方程(2)

教学目标 ①、进一步熟练地解可化为一元一次方程的分式方程.

②、通过分式方程的应用教学，培养学生数学应用意识.

教学重点 让学生学习审明题意设未知数，列分式方程

教学难点　　 在不同的实际问题中，设元列分式方程

分式方程(1)　　　　　　　　

　　　　　　　　　　　　　　　 例：

乘　 最简公分母　　　　　　　　　　　　

整式方程　　　　　　　　　　　　　

小结与作业　 ①、什么是分式方程？举例说明；②、解分式方程的一般步骤：在方程的两边都乘以最简公分母，约去分母，化为整式方程．解这个整式方程．.验根，即把整式方程的根代入最简公分母，看结果是不是零，若结果不是0，说明此根是原方程的根；若结果是0，说明此根是原方程的增根，必须舍去．3、解分式方程为什么要进行验根？怎样进行验根？　 各抒已见畅所欲言说分式方程及其解法，特别要注意验根.

7、有了上面的经验，我们再来完整地解二个分式方程.

例2　解方程：(1)　　　　　　　　 (2)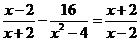　 可先放手让学生自主探索，合作学习并进行总结.深入理解.学生尝试解题，并思考产生增根的原因.总结解分式方程的步骤，并真正理解增根.

板演并小组批改.

6、验根的方法

解分式方程进行检验的关键是看所求得的整式方程的根是否使原分式方程中的分式的分母为零.有时为了简便起见，也可将它代入所乘的整式(即最简公分母)，看它的值是否为零.如果为零，即为增根.

如例1中的x=1，代入x2－1＝0，可知x=1是原分式方程的增根.

5．那么，可能产生“增根”的原因在哪里呢？

4、在将分式方程变形为整式方程时，方程两边同乘以一个含未知数的整式，并约去了分母，有时可能产生不适合原分式方程的解(或根)，这种根通常称为增根.因此，在解分式方程时必须进行检验.