1.根据下列条件写出相应的函数关系式．

(1)直线y＝kx+5经过点(-2,-1)；

(2)一次函数中，当x＝1时，y＝3；当x＝-1时，y＝7．

3.求两个一次函数图象的交点坐标即以两解析式为方程的方程组的解．

2.用一次函数解析式解决实际问题时，要注意自变量的取值范围．

本节课，我们讨论了一次函数解析式的求法

1.求一次函数的解析式往往用待定系数法，即根据题目中给出的两个条件确定一次函数解析式y＝kx+b(k≠0)中两个待定系数k和b的值；

例1 已知一次函数y＝kx+b的图象经过点(-1,1)和点(1，-5),求当x＝5时，函数y的值．

分析 1．图象经过点(-1,1)和点(1，-5)，即已知当x＝-1时，y＝1；x＝1时，y＝-5．代入函数解析式中，求出k与b．

2．虽然题意并没有要求写出函数的关系式，但因为要求x＝5时，函数y的值，仍需从求函数解析式着手．

解 由题意，得

解这个方程组，得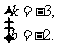

这个函数解析式为y＝-3x-2．

当x＝5时，y＝-3×5-2＝-17．

例2 已知一次函数的图象如下图，写出它的关系式．

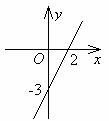
分析 从“形” 看，图象经过x轴上横坐标为2的点，y轴上纵坐标是-3的点．从“数”看，坐标(2,0),(0,-3)满足解析式．

解 设：所求的一次函数的解析式为y＝kx+b(k≠0)．

直线经过点(2,0),(0,-3),把这两点坐标代入解析式,得

　 解得　

所以所求的一次函数的关系式是．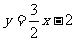

例3 求直线y＝2x和y＝x+3的交点坐标．

分析 两个函数图象的交点处，自变量和对应的函数值同时满足两个函数关系式．而两个函数关系式就是方程组中的两个方程．所以交点坐标就是方程组的解．

解 两个函数关系式组成的方程组为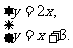

解这个方程组，得

所以直线y＝2x和y＝x+3的交点坐标为(3，6)．

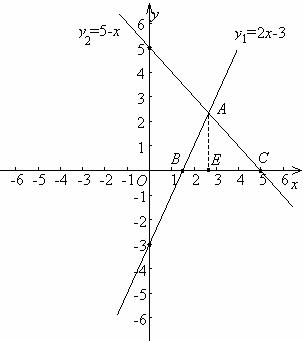
例4 已知两条直线y₁＝2x-3和y₂＝5-x．

(1)在同一坐标系内作出它们的图象；

(2)求出它们的交点A坐标；

(3)求出这两条直线与x轴围成的三角形ABC的面积；

(4)k为何值时，直线2k+1＝5x+4y与k＝2x+3y的交点在每四象限．

分析 (1)这两个都是一次函数，所以它们的图象是直线，通过列表，取两点，即可画出这两条直线．

(2)两条直线的交点坐标是两个解析式组成的方程组的解．

(3)求出这两条直线与x轴的交点坐标B、C，结合图形易求出三角形ABC的面积．

(4)先求出交点坐标，根据第四象限内的点的横坐标为正，纵坐标为负，可求出k的取值范围．

解 (1)

(2)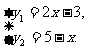　 解得

所以两条直线的交点坐标A为．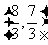

(3)当y₁＝0时，x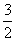＝所以直线y₁＝2x-3与x轴的交点坐标为B(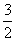，0)，当y₂＝0时，x＝5，所以直线y₂＝5-x与x轴的交点坐标为C(5,0)．过点A作AE⊥x轴于点E，则．

(4)两个解析式组成的方程组为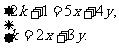

解这个关于x、y的方程组，得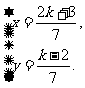

由于交点在第四象限，所以x＞0,y＜0．

即　 解得．

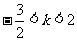上题可作如下分析：

已知y是x的函数关系式是一次函数，则关系式必是y＝kx+b的形式，所以要求的就是系数k和b 的值．而两个已知条件就是x和y的两组对应值，也就是当x＝0时，y＝6；当x＝4时，y＝7.2．可以分别将它们代入函数式，转化为求k与b 的二元一次方程组，进而求得k与b的值．

解 设所求函数的关系式是y＝kx+b(k≠0),由题意，得

解这个方程组，得

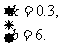
所以所求函数的关系式是y＝0.3x+6．(其中自变量有一定的范围)

讨论 1．本题中把两对函数值代入解析式后，求解k和b的过程，转化为关于k和b的二元一次方程组的问题．

2．这个问题是与实际问题有关的函数，自变量往往有一定的范围．

问题3 若一次函数y＝mx-(m-2)过点(0,3)，求m的值．

分析 考虑到直线y＝mx-(m-2)过点(0,3)，说明点(0,3)在直线上，这里虽然已知条件中没有直接给出x和y的对应值，但由于图象上每一点的坐标(x,y)代表了函数的一对对应值，它的横坐标x表示自变量的某一个值，纵坐标y表示与它对应的函数值．所以此题转化为已知x＝0时，y＝3，求m．即求关于m的一元一次方程．

解 当x＝0时，y＝3．即：3＝-(m-2)．解得m＝-1．

这种先设待求函数关系式(其中含有未知的常数系数)，再根据条件列出方程或方程组，求出未知系数，从而得到所求结果的方法，叫做待定系数法(method 　of undetermined coefficient)．

　 　一次函数关系式y＝kx+b(k≠0)，如果知道了k与b的值，函数解析式就确定了，那么有怎样的条件才能求出k和b呢？

问题1 已知一个一次函数当自变量x＝-2时，函数值y＝-1,当x＝3时，y＝-3．能否写出这个一次函数的解析式呢？

根据一次函数的定义，可以设这个一次函数为:y＝kx+b(k≠0),问题就归结为如何求出k与b的值．

由已知条件x＝-2时，y＝-1，得　 -1＝-2k+b．

由已知条件x＝3时，y＝-3， 得　 -3＝3k+b．

两个条件都要满足，即解关于x的二元一次方程

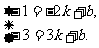　　 　　解得

所以，一次函数解析式为．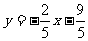

问题2 已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米,求这个一次函数的关系式．

考虑 这个问题中的不挂物体时弹簧的长度6厘米和挂4千克质量的重物时，弹簧的长度7.2厘米,与一次函数关系式中的两个x、y有什么关系？

华氏温标与摄氏温标

　　 温度是热学中最重要的概念之一,温度计的出现标志着热学跨入定量科学的第­一步.

　　 第一支实用温度计,是迁居荷兰的德国玻璃工华伦海特(1686-1736年)制成的.­他把冰、水、氨水和盐的混合物平衡温度定为0°F,冰的熔点定为32°F,而人体的­温度为96°F,1724年,他又把水的沸点定在212°F,后人称这一温标为华氏温标­.1742年,瑞典天文学家摄尔修斯(1701-1744年)用水银作测温物质,以水的沸点为0­℃,冰的熔点为100℃,其间为一百个等分.八年之后,摄尔修斯接受了同事施特默尔­的建议,把两个定点值对调了过来,这就是至今仍广为使用的百分温标,通常又称为­摄氏温标.

十八世纪前半期,实用温度计的制作和应用为十九世纪热学理论的建立提供了­先决条件.毛

　　 ┌────────────────┬────┐

　　 │课题　　　　　　　　　　　　　　 │　　　　 │

　　 │一次函数的性质　　　　　　　　　 │ 投影幕 │

　　 │一次函数性质的应用　　　　　　　 │　　　　 │

　　 └────────────────┴────┘

2.实践探索

　　 (1)实践活动

　　 请收集利用一次函数性质解决实际问题的两个实例,并解答所列举的问题.

　　 (2)巩固练习

　　 课本第62页复习题第14题和15题.