
25,解下列方程组:
(1)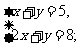 (2)
(2)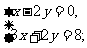
(3)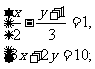 (4)
(4)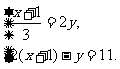
13,已知关于x、y的方程组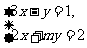 无解,则m的值是( )
无解,则m的值是( )
A.m=-6 B. m=-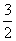 C. m=-
C. m=-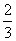 D. m=6
D. m=6
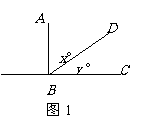
14,如图1,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,设∠ABD和∠DBC的度数分别为x、y,那么下面可以求出这两个角的度数的方程组是( )
A,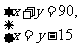 B,
B,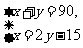 C,
C,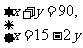 D,
D,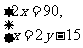
15,已知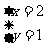 是方程kx-y=3的解,那么k的值是( )
A,2 B,一2 C,1 D,一1
是方程kx-y=3的解,那么k的值是( )
A,2 B,一2 C,1 D,一1
16,某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏本20%,在这项买卖中,这家商店( )
A.赔了8元 B.赚了32元 C.不赔不赚 D.赚了8元
17,已知方程组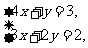 则x-y的值是()
则x-y的值是()
A,1 B,-1 C,0 D,2
18,若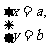 是方程组
是方程组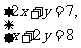 的解,那么a-b的值是( )
的解,那么a-b的值是( )
A.5 B.1 C.-1 D.-5
19,如果x∶y=5∶2,并且满足x-3y=-7,则x、y中较小的是( )
A.35 B.-14 C.-35 D.14
20,某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
|
捐款(元) |
1 |
|
3 |
4 |
||
|
人 数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )
A.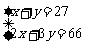 B.
B.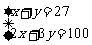 C.
C.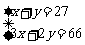 D.
D.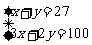
21,今有鸡兔同笼,上有十九头,下有五十八足,则鸡、兔的只数分别是( )
A.鸡9只,兔10只 B.鸡10只,兔10只
C.鸡9只,兔9只 D.鸡10只,兔9只
22,如果方程组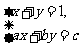 有唯一的一组解,那么a、b、c的值应当满足( )
有唯一的一组解,那么a、b、c的值应当满足( )
A. a=1,c=1 B. a=b=1 C. a≠b D,a=1, c≠1
23,方程3x+y=10的所有正整数解是( )
A.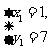 B.
B.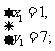
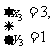
C. 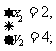
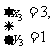 D.
D. 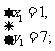
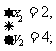
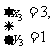
24,某商店经销一种商品,由于进价降低了5%,出售价不变,使得利润由m%提高到(m+6)%,则m的值为( )
A.10 B.12 C.14 D.1
1,已知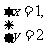 是方程ax-3y=5的一个解,则a=________.
是方程ax-3y=5的一个解,则a=________.
2,已知方程(n-2)x+3y=1是关于x、y的二元一次方程,则n应满足______.
3,若实数m,n满足条件m+n=3,且m-n=1,则m=_____,n=_____.
4,已知等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,则A=___,B=___.
5,某学生在n次考试中,其考试成绩满足:如果最后一次考试得97分,则平均数为90,如果最后一次考试得73分,则平均分为87分,则n=___.
6,方程组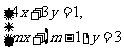 的解x和y的值相等,则m=___.
的解x和y的值相等,则m=___.
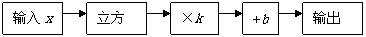 7,给出下列程序:
7,给出下列程序:
且已知当输入的x值为1时,输出值为1;输入的x值为-1时.输出值为-3.则当输入的x值为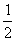 时.输出值为
.
时.输出值为
.
8,若一个二元一次方程的解为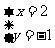 ,则这个方程可以是______(只要求写出一个).
,则这个方程可以是______(只要求写出一个).
9,在关于x1,x2,x3的方程组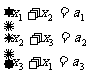 中,已知
中,已知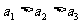 ,那么将x1,x2,x3从大到小排起来应该是____________.
,那么将x1,x2,x3从大到小排起来应该是____________.
10,当x的值为-1,1时,多项式ax2+bx+3的值分别为2,6,则a=____,b=____.
11,将若干只鸡放入若干个笼中,若每个笼中放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,则至少有___只鸡.
12,以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长、井深各几何?若设绳长x尺,井深y尺,则可列方程组为
0.5(x-2)=2
x-2=4
x=6
答:小明一共能租6天。
例5. 辨别下列方程(组),指出哪些是二元一次方程(组)。
(1)3x+y=2xy
(2)5x-2y=6+5x (3)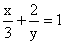 (4)x=y
(4)x=y
(5)5x-3y
(6)x+y+z=3
(7)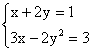
(8)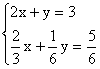 (9)
(9)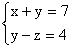 (10)
(10)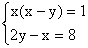
解:二元一次方程有: (4)x=y
二元一次方程组有:(8)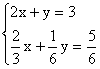
2. 等式的两边都乘以(或除以)同一个数(除数不能为零),所得结果仍是等式.即
如果a=b,那么ac=bc;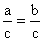 (c≠0)
(c≠0)
求方程的解的过程叫解方程
解一元一次方程的步骤:
①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
以上5个步骤在解一元一次方程时要灵活应用。
问题2:某班同学在植树节时植樟树和白杨树共45棵.已知樟树苗每棵2元,白杨树苗每棵1元,购买这些树苗用了60元.问樟树苗、白杨树苗各买了多少棵?
设:樟树苗买了x棵,白杨树苗买了y棵,根据两种树苗总数为45棵,得
x+y=45, ①
又根据购买树苗的钱数是60元,得
2x+y=60. ②
上面得到的两个方程含有两个未知数(元),并且未知数的次数都是l,像这样的方程叫做二元一次方程.
这里的x、y既要满足树苗总数关系①,又要满足购买树苗钱数关系②,就是说它必须同时满足上面①、②两个方程.因此,我们把上面两个方程加上括号联合在一起,写成:
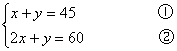
像上面这种由两个一次方程组成的,并且含有两个未知数的方程组叫做二元一次方程组。
[典型例题]
例1. 解方程: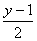 -2=
-2=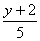
解:去分母:5(y-1)-20=2(y+2)
去括号:5y-5-20=2y+4
5y-25=2y+4
移项: 5y-2y=25+4
合并同类项:3y=29
系数化为1: y=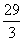
例2. 已知关于x方程(m+2)xm-1+5=0是一元一次方程,求 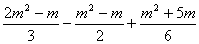 的值。
的值。
分析:此题是求代数式的值,而代数式中含有唯一字母m,所以必须通过前面已知条件求出m,又因为(m+2)xm-1+5=0是一元一次方程,则m-1=1且m+2≠0得m=2,将m=2代入欲求的代数式,即可求得代数式中的值。
解:∵(m+2)xm-1+5=0是一元一次方程
∴m-1=1且m+2≠0
∴m=2
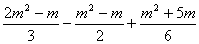
=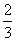 m2-
m2-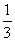 m-
m-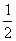 m2+
m2+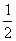 m+
m+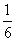 m2+
m2+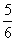 m
m
=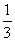 m2+m
m2+m
把m=2代入得:
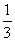 m2+m=
m2+m=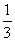 ×22+2=3
×22+2=3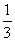
注意,有些同学为计算简便,把欲求代数式中的分母除去(像解方程一样去分母)这就错了,因为方程是等式,可以利用等式的性质;代数式不是等式,不能随意的扩大(或缩小)代数式中的每一项。
例3. 某同学去解方程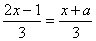 -1在去分母时,方程右边的-1没有乘3,因而求得方程的解为x=2,试求a的值,并正确地解方程。
-1在去分母时,方程右边的-1没有乘3,因而求得方程的解为x=2,试求a的值,并正确地解方程。
分析:这位同学在解题中出现的错误,是常见错误之一,实质上这位同学解的方程是:(2x-1)=(x+a)-1
∴x=2应是方程(2x-1)=(x+a)-1的解
我们应先求a,再求原方程的解
解:这位同学实际解的方程为(2x-1)=(x+a)-1
把x=2代入得:3=2+a-1 ∴a=2
∴原方程为: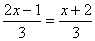 -1
-1
∵2x-1=x+2-3
2x-1=x-1
x=0
∵a=2 ∴方程的解为x=0
例4. 某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0.8元,以后每天收0.5元,小明用身上的3.6元钱租了一张光盘,问他一共能租多少天?
解:设小明一共能租x天
由题意:0.8×2+0.5(x-2)=3.6
知识要点
问题1 王玲今年12岁,她爸爸36岁,问再过几年,她爸爸年龄是她年龄的2倍?
设:再过x年,王玲的年龄是(12+x)岁,她爸爸的年龄为(36+x)岁,是她的年龄的2倍,得:36+x=2(12+x).
上面得到的方程只含有一个未知数(元),并且未知数的次数都是l,像这样的方程叫做一元一次方程.
我们在小学已经学过简单的一元一次方程,知道使方程两边相等的未知数的值叫做方程的解;一元一次方程的解,也可叫做方程的根.
方程是等式,利用等式的性质可以求方程的解.
等式的基本性质是:
1. 等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.即
如果a=b,那么a±c=b±c.
2. 难点:一元一次方程的解法,步骤的灵活运用。
1. 重点:
① 等式的性质
② 运用等式的性质解一元一次方程
③ 理解二元一次方程组的概念
④ 会分析实际问题中蕴含的数量关系,列出二元一次方程组
4. 会根据已知条件列出二元一次方程组。
3. 了解二元一次方程组的概念。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com