
2.初步体会解二元一次方程组的基本思想――“消元”.
1.会用代入法解二元一次方程组.
8.2消元(一)
教学目标:
|
消元(二) 加减消元的概念 例题 加减消元的步骤 代入消元与加减消元 |
引导学生总结出加减消元法的解题思想与步骤,总结出在什么情况下用代入消元还是加减消元法。
加减法和代入法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程,只是消元的方法不同。应根据方程组得具体情况选择更适合它的解法。你会怎样解下面的方程组?
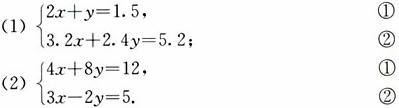
选择你认为最简单的方法解习题8。1中第4题(“鸡兔同笼”)问题。
上面解方程组的过程可以用下面的框图表示:
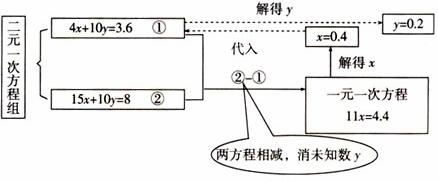
这个框图以用加减法解一个具体的二元一次方程组的过程为例,展示了加减法的解题步骤,以及各步骤的作用。它可以作为加减法解二元一次方程组的一般步骤的典型。
例3 用加减法解方程组

分析:这两个方程中没有同一个未知数的系数相反或相同,直接加减两个方程不能消元。试一试,能否对方程变形,使得两个方程中某个未知数的系数相反或相同。
解:①×3,得
9x+12y=48 ③
②×2,得
10x-12y=66 ④
③+④得
19x=114
x=6
把x=6代入①,得
3×6+4y=16
4y=-2
y=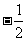
所以,这个方程组的解是
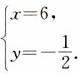
例3中两方程中同一未知数的系数不相等也不相反,所以不能通过直接加减来消元。为消元需要在方程两边乘适当的数,使某个未知数在两方程中的系数相等或相反。
思考
本题如果用加减法消去x应如何解?解得的结果与上面一样吗?
如果要先消x,可以①× 5-②× 3,解方程组时先消哪个未知数都可以,结果是确定的,不会因先消哪个未知数而产生变化。一般地说,先消哪个未知数简便就先消它。例3中,消x,y的运算程度基本相同,不存在先消哪个未知数更简便的情况。
例4 2台大收割机和5台小收割机工作2小时收割小麦3。6公顷,3台大收割机和2台小收割机工作5小时收割小麦8公顷,1台大收割机和1台小收割机1小时各收割小麦多少公顷?
分析:如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机l小时收割小麦______[2]公顷,3台大收割机和2台小收割机1小时收割小麦_____[3]公顷, 由此进一步考虑两种情况下的工作量。
解:设1台大收割机和1台小收割机l小时各收割小麦x公顷和y公顷。
根据两种工作方式中的相等关系,得方程组
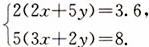
去括号,得
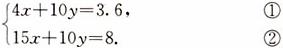
②-①,得
11x=4.4。
解这个方程,得
x=0.4。
把x=0.4代入①,得
y=0.2。
这个方程组的解是
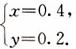
答:1台大收割机和l台小收割机1小时各收割小麦0.4公顷和0.2公顷。
我们知道,可以用代入消元法解方程组

观察
这个方程组的两个方程中,y的系数有什么关系?利用这种关系你能发现新的消元方法吗?
这两个方程中未知数y的系数相同,②-①可消去未知数y,得x=18。
把x=18代入①,得y=4。
思考
联系上面的解法,想一想应怎样解方程组
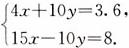
归纳
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法。
这是对加减法的基本步骤的概括,加减法通过两个方程相加或相减实现消元。两方程相加减前应先使要消去的未知数的系数相等或相反,为此需要根据是等式的性质(等式两边乘除相等的量,结果仍相等)先进行必要的方程变形。
|
消元(一) 代入消元法的概念 例题 解题步骤 |
第2课时
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com