6.布置作业：

作业本相应部分

5.回顾与思考

学了本节课你有什么与体会?

设计意图:培养学生的语言表达能力及归纳概括能力，使知识形成体系。

4．联系实际，解决问题:

一块三角形的煎饼，要把它分成大小相等的6块，你有几种不同的分法？

设计意图：一方面是为了应用三角形的中线把三角形分成面积相等的两部分来解决实际际问题，体会数学的应用价值；同时也体现了不同的人得到不同的发展的思想，好的同学可以得到多种分法，培养学生的创新能力。

3．应用新知，体验成功

(1)如图：CD，BE是∆ABC的角平分线，它们相交于点I，则

①∠ACD=∠　　　 =　　　 ∠ACB，∠ABC　　 ∠ABE

②BI是∆　　　 的角平分线，　　　　　　 　　　　　　　

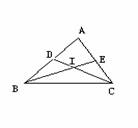
CI是∆　　　　 的角平分线。　　　　　　　　　　　　　

③若∠ABC=60度，∠ACB=80度，则

∠BIC= 　　　度

④你能画出∆ABC的第三条角平分线吗？

(2)、如图：

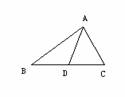
①　　 若AD是∆ABC的中线，

则BD=　　 =　　 BC，BC=　　 BD

②若BD=CD，则AD是∆ABC的　　　　 。

③已知AD是∆ABC的中线，则∆ABD的面积与∆ADC的面积有什么关系？

2．动手实践，探究新知

三角形的角平分线的教学

①事先在黑板上画一个三角形∆ABC，问学生如何画一个角的平分线，比如画∠A的平分线？

学生大约估计到另外两个三角形纸片的作用，于是把问题一提出就要让学生能感知并有一种意识去动手实践，主动探究。我认为能做到这一点就是教学的成功所在。学生利用手上的三角形纸片边操作边与组内其他组员讨论。能引起争论，这是本节课的成功之处。因为这节课理论是可行的，但实际做起来却不一定行。比如，用量角器去画一个角的平分线就存在一个很大的测量误差等。

这样自然引入了三角形的角平分线概念。

并提问：

(1)三角形有几条角平分线？

(2)你发现三角形的三条角平分线有何特点？

设计意图：使学生通过画、折等实践操作活动理解三角形的角平分线概念，并培养学生动手操作能力，自主探索、合作交流，发现三角形的三条角平分线交于一点的规律，体现了知识的获得不是教师传授的，而是学生自己探索得到的。

三角形的中线的教学

在已画的∆ABC的∠A的角平分线AD的基础上提出问题：点D是否是BC的中点？那么什么是线段的中点呢？你有什么方法得到线段的中点呢？

设计意图：由三角形的角平分线自然过渡到三角形的中线，并为下面画三角形的中线作铺垫。这样学生也能自然想到通过折纸的方法马上能找到线段的中点。

再用类似三角形的角平分线、高线的研究方法来研究三角形的中线，三角形的中线是否也有类似的性质呢？

学生动手画、折三角形的中线，观察、猜想、验证。

并提问：

(1)三角形有几条中线？

(2)你发现三角形的三条中线有何特点？

设计意图：通过类比教学三角形的中线，使学生产生知识的迁移，理解三角形的中线的概念，及掌握三角形的三条中线交于一点的性质。

1．回忆旧知，深化提高

(事先让学生准备三个三角形的纸片)

给出一个三角形ABC，请你回忆作出三角形ABC的高。

提问：(1)你用什么作出三角形的高？

(2)高有几条？

(3)你能用折纸的方法找出你准备好的三角形的高吗？

(4)你发现用折纸折出的高与你用三角板画出的高一致吗？

(4)你发现三角形的三条高有何特点？

请同学们拿出已准备好的其中一个三角形纸片，回答以上问题。

2. 教学目标：

(1)知识与技能目标：通过观察、画、折等实践操作、想像、推理、交流等过程，认识三角形的高线、角平分线、中线；会画出任意三角形的高线、角平分线、中线，通过画图、折纸了解三角形的三条高线、三条角平分线、三条中线会交于一点。

(2)过程与方法目标：经历画、折等实践操作活动过程，发展学生的空间观念，推理能力及创新精神。学会用数学知识解决实际问题能力，发展应用和自主探究意识，并培养学生的动手实践能力。

(3)情感与态度目标：通过对问题的解决，使学生有成就感，培养学生的合作精神，树立学好数学的信心。

2.　　 不等式解集的表示方法.

[作业]

必做题:教科书134页习题:2题

教案

指导辨析

总结规律和方法