
见作业纸
5、已知函数y1 = 2 x – 4与y2 = - 2 x + 8的图象,观察图象并回答问题:
(1) x取何值时,2x-4>0?
(2)
 x取何值时,-2x+8>0?
x取何值时,-2x+8>0?
(3) x取何值时,2x-4>0与-2x+8>0同时成立?
(4) 你能求出函数y1 = 2 x – 4与y2 = - 2 x + 8
的图象与X轴所围成的三角形的面积吗?
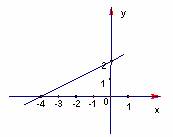
4、如图,直线 是一次函数
是一次函数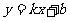 的图象,观察图象,可知:
的图象,观察图象,可知:
(1) ;
;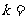 。
。
(2)当 时,
时, 。
。
3、已知函数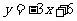 ,当
,当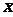 时,
时,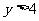 ;
;
当 时,
时, 。
。
2、当自变量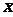 时,函数
时,函数 的值大于0;当
的值大于0;当 时,函数
时,函数 的值小于0。
的值小于0。
1、在一次函数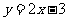 中,已知
中,已知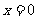 则
则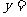 ;若已知
;若已知 则
则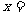 ;
;
例1 如图是一个一次函数,请根据图像回答问题:
(1)当x=0时,y= ,当y=0时,x= ;
(2)写出直线对应的一次函数的表达式 ;
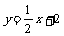

(3)一元一次方程 和一次函数 有什么联系?
例2 画出函数y=-3x+12的图像,利用图像求:
(1)不等式-3x+12>0的解集.(2)不等式-3x+12≤0的解集.
例3某用煤单位有煤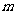 吨,每天烧煤
吨,每天烧煤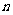 吨,现已知烧煤三天后余煤102吨,烧煤8天后余煤72吨.
吨,现已知烧煤三天后余煤102吨,烧煤8天后余煤72吨.
(1)求该单位余煤量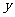 吨与烧煤天数
吨与烧煤天数 之间的函数解析式;
之间的函数解析式;
(2)当烧煤12天后,还余煤多少吨?
(3)预计多少天后会把煤烧完?
例4某人点燃一根长度为25㎝的蜡烛,已知蜡烛每小时缩短5㎝,设xh后蜡烛剩下的长度为y㎝。
(1)、求y与x的函数关系式。
(2)、几个小时以后,蜡烛的长度不足10㎝?
一元一次方程、一次函数的关系
由于任何一元一次方程都可以转化为 的形式,所以解一元一次方程可以转化为:当 时,求 的值。从图象上看,这相当于已知 ,确定 的值。
答:一次函数,函数值确定,与之对应的自变量。纵坐标,横坐标。
一元一次不等式与一次函数的关系
(1)一元一次不等式ax+b>0或ax+b<0(a≠0)是一次函数y=ax+b(a≠0)的函数值 的情形.
(2)直线y=ax+b上使函数值y>0(x轴上方的图像)的x的取值范围是
 ax+b 0的解集;使函数值y<0(x轴下方的图像)的x的取值范围是ax+b
0的解集.
ax+b 0的解集;使函数值y<0(x轴下方的图像)的x的取值范围是ax+b
0的解集.
答:(1)不等于0;(2)>,<。
一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.如果所挂物体的质量为x㎏,弹簧的长度是ycm。
(1)、求y与x之间的函数关系式,并画出函数的图象。
(2)、求弹簧所挂物体的最大质量是多少?
2、请同学们自己编写一道与今天课堂上的例题相似的问题并自己解决。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com