
15.  为何值时,分式方程
为何值时,分式方程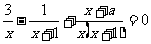 无解?
无解?
解:方程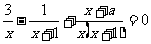 的两边同乘以
的两边同乘以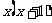 ,去分母,得
,去分母,得
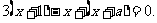
整理,得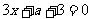 。
。
即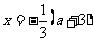 .
.
把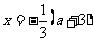 代入最简公分母
代入最简公分母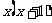 ,使其值为零,说明整式方程的根是增根.
,使其值为零,说明整式方程的根是增根.
当 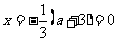 时,
时,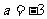 ;
;
当 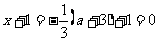 时,
时,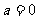 .
.
于是当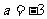 或
或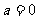 时原分式方程无解.
时原分式方程无解.
14.解方程:
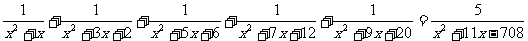 .
.
解:因为方程的左边
 故原方程可变为
故原方程可变为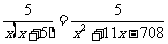 .
.
所以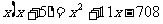 .
.
解得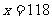 .
.
经检验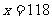 是原方程的根.
是原方程的根.
13. 已知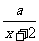 与
与 的和等于
的和等于 ,求
,求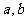 之值.
之值.
解:根据题意,有
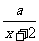 +
+ =
= .
.
去分母,得
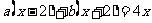 .
.
去括号,整理得
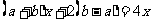 .
.
比较两边多项式系数,得
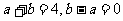 .
.
解得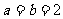 .
.
12.设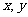 是两个不同的正整数,且
是两个不同的正整数,且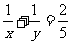 ,则
,则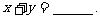
解:由条件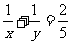 得
得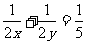 .
.
显然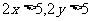 ,故可设
,故可设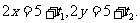
则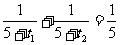 .去分母并整理,得
.去分母并整理,得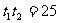 .
.
因为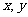 是两个不同的正整数,所以
是两个不同的正整数,所以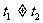 .
.
所以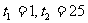 或
或 .
.
所以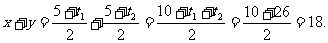
11. 若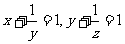 ,则
,则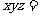 _____.
_____.
解:由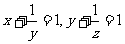 ,得
,得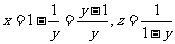 .
.
所以 .
.
10. 若关于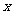 的方程
的方程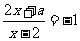 的解为正数,则
的解为正数,则 的取值范围是_____.
的取值范围是_____.
解:由方程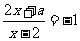 ,得
,得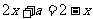 ,从而
,从而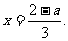
又由题意,得 所以
所以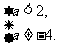
故 的取值范围是
的取值范围是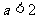 且
且 .
.
9.方程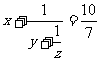 的正整数解
的正整数解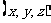 是_____.
是_____.
解:由 ,得
,得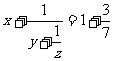 .
.
因为是正整数,故必有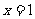 ,因而
,因而
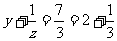 .
.
又因为 也是正整数,故又必有
也是正整数,故又必有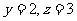 .
.
经检验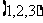 是原方程的根.
是原方程的根.
因此,原方程的正整数解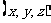 是
是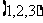 .
.
8. 已知: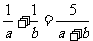 ,则
,则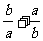 的值为_____.
的值为_____.
解: 由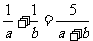 ,得
,得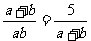 .
.
所以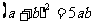 .
.
所以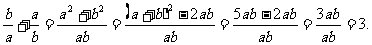
7.已知: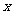 满足方程
满足方程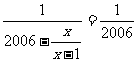 ,则代数式
,则代数式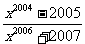 的值是_____.
的值是_____.
解:由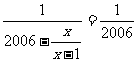 ,得
,得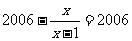 .
.
所以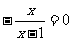 .所以
.所以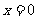 .
.
经检验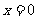 满足原方程.
满足原方程.
故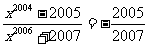 .
.
6.设轮船在静水中的速度为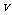 ,该船在流水(速度为
,该船在流水(速度为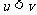 )中从上游A驶往下游B,再返回A,所用的时间为T,假设
)中从上游A驶往下游B,再返回A,所用的时间为T,假设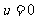 ,即河流改为静水,该船从A至B再返回A,所用时间为
,即河流改为静水,该船从A至B再返回A,所用时间为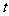 ,则( )
,则( )
(A)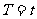 (B)
(B)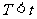 (C)
(C)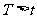 (D)不能确定T与
(D)不能确定T与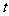 的大小关系
的大小关系
解:设 相距为
相距为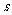 ,则
,则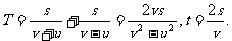
所以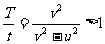 ,即
,即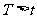
故选(C)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com