
39.解析:设王老师步行的速度是x千米/时,则骑自行车的速度是3x千米/时, 20分钟=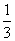 小时,由题意,得
小时,由题意,得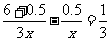 ,解得x=5.经检验x=5是所列方程的根,∴3x=3×5=15(千米/时).答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时.点评:①王老师骑自行车接小刚所走路程易错以为是(3+0.5)千米.
②行程问题中的单位不统一是个易忽略点.
,解得x=5.经检验x=5是所列方程的根,∴3x=3×5=15(千米/时).答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时.点评:①王老师骑自行车接小刚所走路程易错以为是(3+0.5)千米.
②行程问题中的单位不统一是个易忽略点.
38.解析:设甲队单独完成此项工程需2x天,则乙队需要3x天,由题意,得
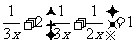 , 解之得x=2,经检验,x=2是所列分式方程的根.∴2x=2×2=4,3x=3×2=6.答:甲队单独完成需4天,乙队需6天.点拨:①本题使用了“参数法”, 当题目中出现两个量的比值时,使用这一方法比较简便;②因为效率与时间成反比, 所以本题易错设为:“甲单独完成需3x天,乙需2x天”;③验根极易被忽略.
, 解之得x=2,经检验,x=2是所列分式方程的根.∴2x=2×2=4,3x=3×2=6.答:甲队单独完成需4天,乙队需6天.点拨:①本题使用了“参数法”, 当题目中出现两个量的比值时,使用这一方法比较简便;②因为效率与时间成反比, 所以本题易错设为:“甲单独完成需3x天,乙需2x天”;③验根极易被忽略.
37.(1)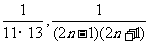 .(2)分式减法,对消
.(2)分式减法,对消
(3)解析:将分式方程变形为
整理得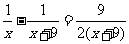 ,方程两边都乘以2x(x+9),得2(x+9)-2x=9x,解得x=2.
,方程两边都乘以2x(x+9),得2(x+9)-2x=9x,解得x=2.
经检验,x=2是原分式方程的根.
点评:此方程若用常规方法来解,显然很难, 这种先拆分分式化简后再解分式方程的方法不失是一种技巧.
34.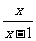 ,
,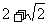 35.
35.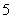 36.
36.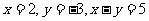
33.解析:原方程可变形为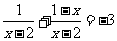 .方程两边都乘以最简公分母(x-2),得1+1-x=-3(x-2),解这个整式方程, 得x=2,把x=2代入公分母,x-2=2-2=0,x=2是原方程的增根,所以,原方程无实数解.
.方程两边都乘以最简公分母(x-2),得1+1-x=-3(x-2),解这个整式方程, 得x=2,把x=2代入公分母,x-2=2-2=0,x=2是原方程的增根,所以,原方程无实数解.
点评:验根是解分式方程的易忽略点.
31 解析:原式=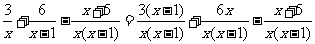
=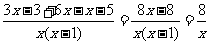 .
.
点评:①学习了解分式方程之后,在进行分式的化简计算时, 易错将本该通分的运算变成了去分母;②进行分式的化简计算应进行到最简分式为止,本题还易错将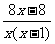 当成最后结果.
当成最后结果.
32.解析:原式=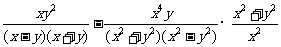
=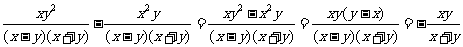 .
.
点评:熟练而准确的因式分解是进行分式化简的重要保证,分式的加、减、乘、除混合运算易出现运算顺序方面的错误.
30.D(点拨:甲和乙的工作效率分别是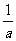 ,
,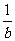 ,合作的工作效率是
,合作的工作效率是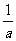 +
+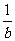 ,所以,合作完成需要的时间是
,所以,合作完成需要的时间是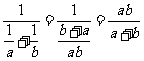 )
)
29.B(点拨:移项,得ax-3x=-5,∴(a-3)x=-5,∴x=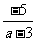 ,∵
,∵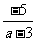 <0,∴a-3>0,a>3.解分式不等式应根据有理数除法的负号法则,即
<0,∴a-3>0,a>3.解分式不等式应根据有理数除法的负号法则,即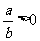 ,则有
,则有 或
或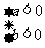 ;若
;若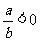 , 则有
, 则有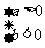 或
或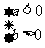 ,然后通过解不等式或不等式组得到相关字母的取值范围)
,然后通过解不等式或不等式组得到相关字母的取值范围)
28.B(点拨:方程两边都乘以d(b-x),得d(x-a)=c(b-x),∴dx-da=cb-cx,(d+c)x=cb+da,
∴当d+c≠0,即c≠-d时,原方程有解)
27.B(点拨:原式=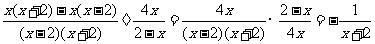 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com