
4.若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是( )
A.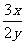 B.
B.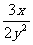 C.
C.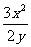 D.
D.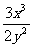
3.化简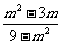 的结果是( )
的结果是( )
A.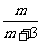 B.
B.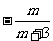 C.
C.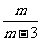 D.
D.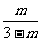
2.下列计算正确的是( )
A.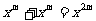 B.
B.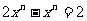 C.
C.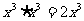 D.
D.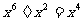
1.下列各式: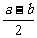 ,
,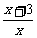 ,
,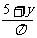 ,
,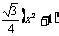 ,
,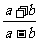 ,
,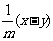 中,是分式的共有( )
中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
[知识点解析]:把几个异分母分式分别化为与原分式值相等的同分母分式,叫做分式的通分.
[方法指导]:先求出所有分式分母的最简公分母,再将所有分式的分母变为最简公分母.同时各分式按照分母所扩大的倍数,相应扩大各自的分子.
[例题解析]:若分式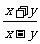 中的x、y的值都变为原来的3倍,则此分式的值( )
中的x、y的值都变为原来的3倍,则此分式的值( )
A、不变 B、是原来的3倍 C、是原来的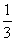 D、是原来的
D、是原来的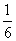
七 分式的四则运算
[知识点解析]:1.同分母分式加减法则:分母不变,将分子相加减. 2.异分母分式加减法则:通分后,再按照同分母分式的加减法法则计算. 3.分式的乘法法则:用分子的积作分子,分母的积作分母. 4.分式的除法法则:把除式变为其倒数再与被除式相乘.
[方法指导]:注意一定要按运算顺序运算。
[例题解析]:例1.计算: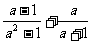 .
.
[详解]:解法1:原式=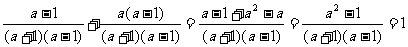 .
.
解法2:原式=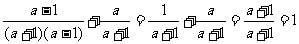 .
.
[注意]:异分母分式的加减法可用通分后再加减;若能先约分的,则先化简,一般可起到简便运算的效果.
例2.化简: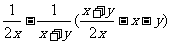
[详解]:解法1:原式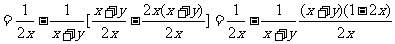
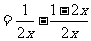
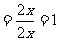
解法2:原式
[注意]:本题可按运算顺序先算括号再乘除后加减;或利用乘法分配率起到简便运算功效.
例3.先化简代数式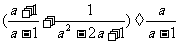 ,然后选取一个使原式有意义的a值代入求值.
,然后选取一个使原式有意义的a值代入求值.
[详解]:原式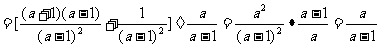 .
.
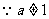 且
且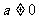 ,若
,若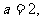 则原式
则原式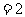 .
.
[注意]:若原题改为先化简代数式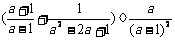 ,然后选取一个你喜欢的a的值代入求值.则化简得原式
,然后选取一个你喜欢的a的值代入求值.则化简得原式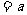 ,但仍然要考虑使原式有意义,即
,但仍然要考虑使原式有意义,即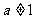 且
且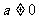 .
.
例4.先化简,再求值: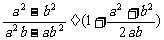 ,其中
,其中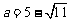 ,
,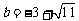 .
.
[详解]:原式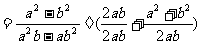
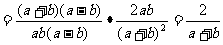
当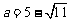 ,
,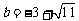 时,原式
时,原式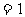 .
.
[注意]:分式的除法没有分配律,避免出现原式 的错误
的错误
例5.已知实数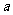 满足
满足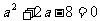 ,求
,求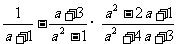 的值.
的值.
[详解]:化简得原式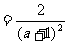 由
由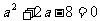 知,
知,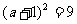 ;
;
[注意]:整体代入,起到降次化简的显著效果.
[精典练习]1. 计算:
(1)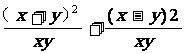 ;(2)
;(2)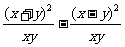
4.所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母
[精典练习]分式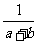 、
、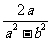 、
、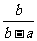 的最简公分母为( D ).
的最简公分母为( D ).
(A)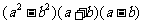 (B)
(B)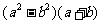 (C)
(C)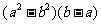 (D)
(D)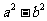
3.相同字母(或因式)的幂取指数最大的;
2.各分式的分母中所有字母或因式都要取到;
1.取各分式的分母中系数最小公倍数;
[知识点解析]:一个分式的分子和分母没有公因式时,这个分式称为最简分式.约分时,一般将一个分式化为最简分式.
[方法指导]:1.最简分式的分子分母不能再同时整除一个式子或字母、数字。
2.最简公分母的确定方法:系数取各因式系数的最小公倍数,相同字母的最高次幂及单独字母的幂的乘积.
[例题解析]:例1.求分式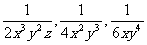 的(最简)公分母。
的(最简)公分母。
[详解]:对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x3,字母y为底的幂的因式,取其最高次幂y4,再取字母z。所以三个分式的公分母为12x3y4z。
例2. 求分式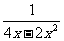 与
与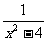 的最简公分母。
的最简公分母。
[详解]:先把这两个分式的分母中的多项式分解因式,即
4x-2x2= -2x(x-2),x2-4=(x+2)(x-2),
把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即
2x(x+2)(x-2)就是这两个分式的最简公分母。
[注意]:找最简公分母的步骤:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com