
1. 二元一次方程和一次函数的关系。
2、数形结合的思想。“以图识性,以性作图”。在研究函数的过程中,初中阶段着重于由描点法作出函数图象,通过对函数图象的观察,更直观地寻求函数的性质.而在今后高中阶段的学习中,将着重于通过函数解析式考查其性质,依性质有目的的选点作图。对于函数的性质,我们要结合图象记忆、理解、应用。
实践与探索1
教学目标
知识要求:初步理解二元一次方程与一次函数的关系,能根据一次函数的图象求二元一次方程组的近似解。掌握运用二元一次方程和一次函数解决实际问题的方法。培养同学们分析问题、运用所学的知识解决实际问题的能力;体会对应关系和数形结合思想。
教学重点:
本节课我们研究了反比例函数的图象及性质,从中学到了哪些数学思想和方法呢?
1、类比的思想方法.正比例函数和反比例函数是小学正比例关系和反比例关系的扩充。对于发展了的事物,既有遗传性,又有变异性,因此我们要注意到它们之间的联系,共同点和不同点.而正比例函数和反比例函数在定义、图象及性质上又有相同点和不同点。请同学们课下自己总结。
2、反比例函数的性质:
教师引导学生对比正比例函数的性质,观察反比例函数的图象并回答以下问题:
反比例函数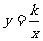 (
( ≠0),当
≠0),当 >0时,图象分布在哪些象限?当
>0时,图象分布在哪些象限?当 <0时,图象分布在哪些象限?理由是什么。
<0时,图象分布在哪些象限?理由是什么。
从图象判断:横纵坐标符号相同时图象在第一、三象限,横纵坐标符号相异时图象在第二、四象限。
从解析式判断:当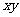 >0时,
>0时, 与
与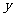 同号,图象在第一、三象限,当
同号,图象在第一、三象限,当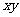 <0时,
<0时, 与
与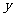 异号,图象在第二、四象限。
异号,图象在第二、四象限。
(2)当 >0时,随着
>0时,随着 值的增大,
值的增大,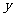 的值有何变化?
的值有何变化? <0呢?
<0呢?
教师和学生一起由图象和列表观察: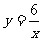 从表中看,
从表中看, 从小到大变化时,
从小到大变化时,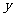 的值减小。从图上看:
的值减小。从图上看: 从左到右增加时,
从左到右增加时,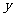 的值从大到小。
的值从大到小。
(3)图象与坐标轴的接近程度?
因为 ≠0,
≠0,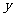 ≠0,所以图象与
≠0,所以图象与 轴和
轴和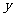 轴没有交点。
轴没有交点。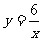 中
中 与
与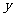 同号,故图象不会穿过坐标轴分布在第二、四象限。
同号,故图象不会穿过坐标轴分布在第二、四象限。
反比例函数的性质:
(1)当 >0时,函数图象的两个分支分别分布在第一、三象限内,在每一个象限中,
>0时,函数图象的两个分支分别分布在第一、三象限内,在每一个象限中,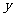 随
随 的增大而减小;当
的增大而减小;当 <0时,两个分支分别分布在第二、四象限内,在每一个象限中,
<0时,两个分支分别分布在第二、四象限内,在每一个象限中,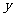 随
随 的增大而增大。
的增大而增大。
(2)两个分支都无限接近但永远不能达到 轴和
轴和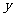 轴。
轴。
1、反比例函数的图象
例 作反比例函数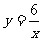 和
和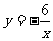 的图象
的图象
方法:第一步,确定 的取值范围(
的取值范围( ≠0)先给出
≠0)先给出 >0的一些值,然后启发学生从解析式推断出
>0的一些值,然后启发学生从解析式推断出 <0的情况.适当取点列表,以保证图象的精确性和整体轮廓;第二步,在直角坐标系里标出每一对实数(
<0的情况.适当取点列表,以保证图象的精确性和整体轮廓;第二步,在直角坐标系里标出每一对实数( ,
,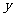 )所对应的点;第三步,用一条平滑曲线根据自变量由小到大的顺序把这些点连结起来。
)所对应的点;第三步,用一条平滑曲线根据自变量由小到大的顺序把这些点连结起来。
解:先作反比例函数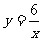 的图象
的图象
 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
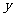 |
… |
-1 |
-1.2 |
-1.5 |
-2 |
-3 |
-6 |
6 |
3 |
2 |
1.5 |
1.2 |
1 |
… |
解:再作反比例函数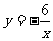 的图象
的图象
 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
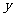 |
… |
1 |
1.2 |
1.5 |
2 |
3 |
6 |
-6 |
-3 |
-2 |
-1.5 |
-1.2 |
1 |
… |
分别描点画图如下:


教师归纳总结
(1)反比例函数的图象是双曲线,图象关于原点成中心对称。列表时自变量的值可以选取绝对值相等而符号相反的数(如±1,±2等等)相应地就得到绝对值相等而符号相反的对应的函数值.这样即可以简化计算的手续,又便于在坐标平面内找到点。
(2)反比例函数的图象的两支都无限地接近但永远不能达到 轴和
轴和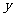 轴,所以图象与
轴,所以图象与 轴
轴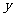 轴没有交点.如果发现画的图象“无限接近”坐标轴后,又偏离坐标轴,这也是错误的,教师可在课堂上演示,并说明错误的原因。
轴没有交点.如果发现画的图象“无限接近”坐标轴后,又偏离坐标轴,这也是错误的,教师可在课堂上演示,并说明错误的原因。
(3)在解实际问题时,应先确定 的取值范围,这时画出的图象就不一定是两个分支,曲线可能只是局部的。
的取值范围,这时画出的图象就不一定是两个分支,曲线可能只是局部的。
2、 如何画一次函数,正比例函数的图象?那么反比例函数呢?
1、 什么叫一次函数?什么叫正比例函数?什么叫反比例函数?
4、培养学生用“数形结合”的思想与方法解决数学问题。
教学重点和难点
反比例函数的图象的画法和性质是本节的重点,函数增减性的理解是本节的难点。
教学过程
3、能结合图象理解反比例函数的性质。
2、使学生能根据问题中的条件确定反比例函数的解析式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com