2、能画出简单函数的图象，会列表、描点、连线；

　数轴上的点与实数间的关系是什么？

引出: 对于坐标平面内任意一点，有唯一的一对有序实数与它对应；对于任意一对有序实数，坐标平面内有唯一的一点与它对应。也就是说，坐标平面内的点与有序实数对是-一对应的　

例3 指出下列各点所在象限或坐标轴:

A(-2 ,3) ,B(1 , -2) C( -1 ,- 2) ,D( 3 , 2) ,E(-3 ,0 ) ,F( 0 , 1)

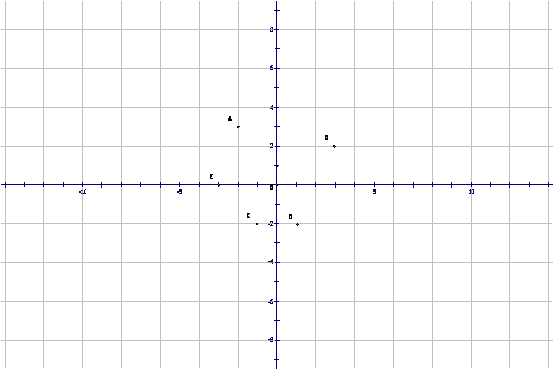
大家由此例题可以看出,B, C两点是什么关系?

引导学生指出：B,C点分别是关于y轴对称．然后，进一步引导学生总结出，若P(a，b)，则P点关于x轴对称点P₁的坐标：横坐标与P的横坐标相同，纵坐标绝对值相等，符号相反，即P₁(a，-b)； P点关于y轴的对称点P₂点的坐标；横坐标与P点横坐标绝对值相等，符号相反，纵坐标与P点纵坐标相同，即P₂(-a，b)；P点关于原点的对称点坐标：横纵坐标与P点的横纵坐标绝对值相等，符号相反，即P3(-a，-b)．

　对称点的坐标可归纳成下表

　例4 已知A(2，y₁)、B(x₂，-3)，根据下列条件，求出A、B点坐标．

　(1)A、B关于x轴对称；

　(2) A、B关于y轴对称；

　(3) A、B关于原点对称．

　解：(1)因为A、B关于x轴对称，它们横坐标相同，纵坐标互为相反数，所以x₂=2，y₁=3，则A(2，3)，B(2，-3)．

　(2)因为A、B关于y轴对称，它们横坐标互为相反数，纵坐标相同，所以，x₂=-2，y₁=-3，则A(2，-3)，B(-2，-3)．

　(3)因为A、B关于原点对称，它们的横纵坐标都互为相反数，所以x₂=-2，y₁=3，则A(2，3)，B(-2，-3)．

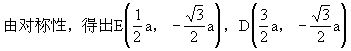
　例5 如图11，平行四边形ABCD中，A在坐标原点，D在第一象限角平分线上,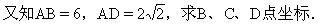　

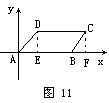
　分析：因为D点在第一象限角平分线上，所以D点的横坐标与纵坐标相同，又D、C在平行x轴直线上，所以D、C点纵坐标相同，结合平行四边形性质，即可求出各顶点坐标了．

　在引导学生分析的基础上，由同学们完成此题，D(2，2)、C(8，2)、B(6，0)．

　例3和例4都是在给定的坐标系中求几何图形中某些点的坐标，要提醒同学们，平面内同一个点，如果坐标系选择不同(即坐标原点的位置不同)，在不同的坐标系中对应的坐标也不同；反之，同一个有序实数对(x，y)，在不同的坐标系中，对应的点也不同．因此，使学生们进一步理解到只有在给定的坐标系中，平面内的点与有序实数对才是一一对应的．

　　小结：

(1)根据坐标找出平面内的点

　(2)关于x轴对称的两点，横坐标相同，纵坐标互为相反数.关于y轴对称的两点，横坐标互为相反数，纵坐标相同.

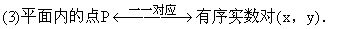
函数的表示法与函数的图象

教学目标：

1、知道函数图象的意义；

3．什么是轴对称图形？什么是中心对称图形？

　数轴上的点与实数间的关系是什么？

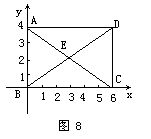
2．已知长方形ABCD，边长分别为6和4，如图8，求其四个顶点坐标；对角线交点坐标．

1．口答填空

　平面直角坐标系的建立是在平面内取______两条数轴；取______为正方向；两条数轴的______相同；

　所有横标为O的点在______上；

　所有纵标为O的点在______上；

　所有横、纵坐标相等的点在______上；

　所有横、纵坐标互为相反数的点在______上；

　P(x，y)为第一象限内的点，则x______，y______；

　P(x，y)为第二象限内的点，则x______，y______；

　P(x，y)为第三象限内的点，则x_______，y______；

　P(x，y)为第四象限内的点，则x______，y______．

3．能熟练地指出某些几何图形在坐标平面内一些点的坐标．

　数学重点和难点

　使学生灵活运用平面直角坐标系的基础知识解决求几何图形中一些点的坐标问题，初步体会和掌握用代数的方法解决几何问题的思维方法．

　教学过程

2.使学生掌握平面内一点关于x轴，y轴及原点的对称点的坐标．

　　 分析:由(1)和(2)总结出：一般地x轴上点的坐标表示为P(x，0)，y轴上点的坐标表示为P(0，y).(3),(4)省略.

　小结：

(1)如何建立平面直角坐标系．

　(2)各象限内的点及x轴，y轴上的点的特征．

平面直角坐标系(二)

　教学目的

1.掌握平面内的点与有序实数对的一一对应关系，并能熟练地根据坐标找出平面内的点.

2． 学生已经知道两个实数可以表示平面内的点，图1中的点M，N的坐标如何表示呢？

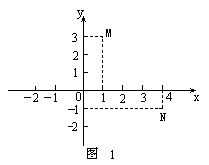
　由M点向x轴和y轴分别引垂线，垂足在x轴坐标为1，在y轴坐标为3，一对实数1，3就表示了M点的位置，1叫M点的横坐标，3叫M点的纵坐标，记作M(1，3)，容易得到N点坐标为(4，－1)，特别要指出：一个点的横纵坐标不能写颠倒，(1，3)和(3，1)是两组不同的实数对，表示平面内不同的点．

　由学生回答，若给出实数对(－2，2)，(3，－2)，如何在坐标系中找出对应的点，并把点画在图1中．

　　例1 在坐标系中，如图2，指出A点、B点、C点坐标,同时指出各点所在的象限．

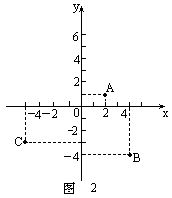
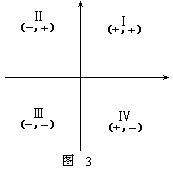
　由上面的例1引导学生总结出四个象限内点的坐标的特征，并画出图3帮助同学们记忆．

　例2 在坐标平面内，

　(1)x轴上点的纵坐标有什么特点？

　(2)y轴上点的横坐标有什么特点？

1．平面直角坐标系的建立

　向学生提出问题：

　王敏同学在教室内座位的位置，能否用所在的行和排来确定呢？

　通过这个问题，使学生明白用两个实数就可以表示出平面内点的位置．

　如何在平面内建立直角坐标系呢？让学生看课本中的有关段落，然后向学生提出问题．

　(1)如何建立平面直角坐标系？在学生回答的基础上强调以下三句话：在平面内取互相垂直有公共原点的两条数轴；取向右，向上的方向为正方向；两条数轴的单位长度相同．

　(2)指出坐标系中各部分的名称(x轴，y轴，原点及第一、二、三、四象限)．

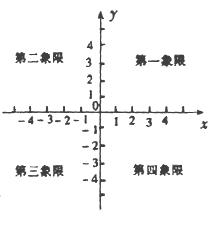
　(3)x轴及y轴上的点属于哪个象限？