1.平面直角坐标系的有关概念及画法；

例1 在上图中分别描出坐标是(2,3)、(－2,3)、(3,－2)的点Q、S、R，Q(2,3)与P(3,2)是同一点吗？S(－2,3)与R(3,－2)是同一点吗？解

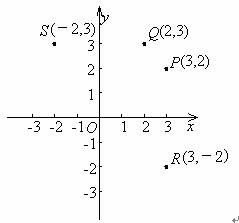
Q(2,3)与P(3,2)不是同一点；

S(－2,3)与R(3,－2)不是同一点．

例2 写出图中的点A、B、C、D、E、F的坐标．观察你所写出的这些点的坐标，回答：(1)在四个象限内的点的坐标各有什么特征？

(2)两条坐标轴上的点的坐标各有什么特征？

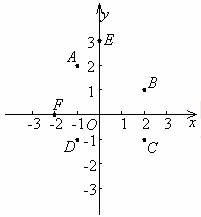
解 A(－1,2)、B (2,1)、C (2,－1)、D (－1,－1)、E (0,3)、F (－2,0)．

(1)在第一象限内的点,横坐标是正数,纵坐标是正数；

在第二象限内的点,横坐标是负数,纵坐标是正数；

在第三象限内的点,横坐标是负数,纵坐标是负数；

在第四象限内的点,横坐标是正数,纵坐标是负数；

(2)x轴上点的纵坐标等于零；

y轴上点的横坐标等于零．

说明 从上面的例1、例2可以发现直角坐标系上每一个点的位置都能用一对有序实数表示，反之，任何一对有序实数在直角坐标系上都有唯一的一个点和它对应．也就是说直角坐标系上的点和有序实数对是一一对应的．

例3 在直角坐标系中描出点A(2,－3)，分别找出它关于x轴、y轴及原点的对称点，并写出这些点的坐标．观察上述写出的各点的坐标，回答：

(1)关于x轴对称的两点的坐标之间有什么关系？

(2)关于　y轴对称的两点的坐标之间有什么关系？

(3)关于原点对称的两点的坐标之间又有什么关系？

解

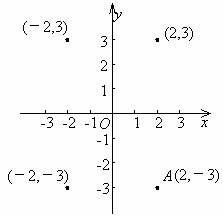
(1)关于x轴对称的两点：横坐标相同，纵坐标绝对值相等，符号相反；

(2)关于y轴对称的两点：横坐标绝对值相等，符号相反，纵坐标相同；

(3)关于原点对称的两点：横坐标绝对值相等，符号相反，纵坐标也绝对值相等，符号相反．

例4 在直角坐标平面内，(1)第一、三象限角平分线上点的坐标有什么特点？(2)第二、四象限角平分线上点的坐标有什么特点？

分析　如图，P为第一、三象限角平分线上位于第一象限内任一点，作PM⊥x轴于M，在Rt△PMO中，∠1＝∠2＝45°，所以｜OM｜=｜MP｜，则P点的横坐标，纵坐标绝对值相等，又因为P点位于第一象限内，OM为正值，MP也为正值，所以P点横坐标与纵坐标相同．同样若P点位于第三象限内，则OM为负值，MP也为负值，所以P点横坐标与纵坐标也相同．若P点为第二、四象限角平分线上任一点，则OM与MP一正一负，所以P点横坐标与纵坐标互为相反数．

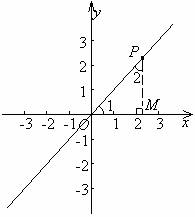
解 (1)第一、三象限角平分线上点：横坐标与纵坐标相同；

问题1 例如你去过电影院吗？还记得在电影院是怎么找座位的吗？

解 因为电影票上都标有“×排×座”的字样，所以找座位时，先找到第几排，再找到这一排的第几座就可以了．也就是说，电影院里的座位完全可以由两个数确定下来．

问题2 在教室里，怎样确定一个同学的座位？

解 例如，××同学在第3行第4排．这样教室里座位也可以用一对实数表示．

问题3 要在一块矩形ABCD(AB＝40mm，AD＝25mm)的铁板上钻一个直径为10mm的圆孔，要求：

(1)孔的圆周上的点与AB边的最短距离为5mm，

(2)孔的圆周上的点与AD边的最短距离为15mm．

试问：钻孔时，钻头的中心放在铁板的什么位置？

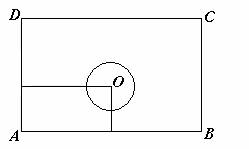
分析 圆O的中心应是钻头中心的位置．因为⊙O直径为10mm，所以半径为5 mm，所以圆心O到AD边距离为20mm，圆心O到AB边距离为10mm．由此可见，确定一个点(圆心O)的位置要有两个数(20和10)．

在数学中，我们可以用一对有序实数来确定平面上点的位置．为此，在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图)，这就建立了平面直角坐标系(rightangled coordinates system)．通常把其中水平的一条数轴叫做x轴或横轴，取向右为正方向；铅直的数轴叫做y轴或纵轴，取向上为正方向；两数轴的交点O叫做坐标原点．

在平面直角坐标系中，任意一点都可以用一对有序实数来表示．例如，图中的点P，从点P分别向x轴和y轴作垂线，垂足分别为M和N．这时，点M在x轴上对应的数为3，称为点P的横坐标(abscissa)；点N在y轴上对应的数为2，称为点P的纵坐标(ordinate)．依次写出点P的横坐标和纵坐标，得到一对有序实数(3,2)，称为点P的坐标(coordinates)．这时点P可记作P(3,2)．　在直角坐标系中，两条坐标轴把平面分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域，分别称为第一、二、三、四象限．坐标轴上的点不属于任何一个象限．

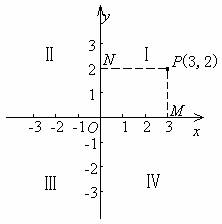
如图是一条数轴，数轴上的点与实数是一一对应的．数轴上每个点都对应一个实数，这个实数叫做这个点在数轴上的坐标．例如，点A在数轴上的坐标是4，点B在数轴上的坐标是－2.5．知道一个点的坐标，这个点的位置就确定了．

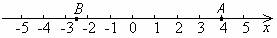
我们学过利用数轴研究一些数量关系的问题，在实际生活中．还会遇到利用平面图形研究数量关系的问题．

课本第29页的第3、4、5、6题．

通过本节课的学习，一方面，我们进一步认识了如何列函数关系式，对于几何问题中列函数关系式比较困难，有的题目的自变量的取值范围也很难确定，只有通过一定量的练习才能做到熟练地解决这个问题；另一方面，对于用数学式子表示的函数关系式的自变量的取值范围，考虑两个方面，其一是分母不能等于0，其二是开偶次方的被开方数是非负数．

课本第28页练习的第1、2、3题

3．函数值

　 例2．在上面的练习(3)中，当MA＝1cm时，重叠部分的面积是多少?

请同学们求一求在例1中当x=5时各个函数的函数值．

2．用数学式子表示的函数的自变量取值范围

例1．求下列函数中自变量x的取值范围

(1)y=3x－l　　 (2)y＝2x²+7　 (3)y=　　 (4)y=

　　 分析：用数学表示的函数，一般来说，自变量的取值范围是使式子有意义的值，对于上述的第(1)(2)两题，x取任意实数，这两个式子都有意义，而对于第(3)题，(x+2)必须不等于0式子才有意义，对于第(4)题，(x－2)必须是非负数式子才有意义．

1．实际问题中的自变量取值范围

问题1：在上面的联系中所出现的各个函数中，自变量的取值有限制吗?如果有．各是什么样的限制?

问题2：某剧场共有30排座位，第l排有18个座位，后面每排比前一排多1个座位，写出每排的座位数与这排的排数的函数关系式，自变量的取值有什么限制。

　　 从右边的分析可以看出，第n排的　 　排数　　 座位数

　　 座位　 　　　　　　　 l　 　 18

一方面可以用18+(n－1)表　　　2　　18+1

3　　18+2

　　 示，另一方面可以用m表示，所以　 　…　　…

　　 m＝18+(n－1)　 　　　　　 n　　 18+(n－1)

n的取值怎么限制呢?显然这个n也应该取正整数，所以n取1≤n≤30的整数或0<n<31的整数。请同学们试着写出上面第2、3两个问题中自变量的取值范围。