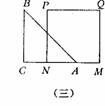
3．如图(三)，等腰直角三角形ABC边长与正方形MNPQ的边长均为l0cm，AC与MN在同一直线上，开始时A点与M点重合，让△ABC向右运动，最后A点与N点重合。试写出重叠部分面积y与长度x之间的函数关系式．

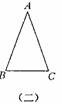
2．如图(二)，请写出等腰三角形的顶角y与底角x之间的函数关系式．

1．填写如右图(一)所示的加法表，然后把所有填有10的格子涂黑，看看你能发现什么?如果把这些涂黑的格子横向的加数用x表示，纵向加数用y表示，试写出y关于x的函数关系式。

课本第28页习题17.1第1、2题。

关于函数的定义的理解应注意两个方面，其一是变化过程中有且只有两个变量，其二是对于其中一个变量的每一个值，另一个变量都有惟一的值与它对应．对于实际问题，同学们应该能够根据题意写出两个变量的关系，即列出函数关系式。

课本第26页练习的第1、2，3题，

例1．用总长60m的篱笆围成矩形场地，求矩形面积S(m²)与边l(m)之间的关系式，并指出式中的常量与变量，自变量与函数。

例2．下列关系式中，哪些式中的y是x的函数?为什么?

(1)y＝3x+2　　 (2)y²＝x　　 (3)y＝3x²+x+5

3．表示函数的方法

　　 (1)解析法，如问题2、问题3、问题4中的s＝30t、V=2 R3、l＝，这些表达式称为函数的关系式，

　　 (2)列表法，如问题4中的波长与频率关系表；

(3)图象法，如问题l中的气温与时间的曲线图．

2．函数的概念

　　 上面的各个问题中，都出现了两个变量，它们相互依赖，密切相关，例如：

　　 在上述的第1个问题中，一天内任意选择一个时刻，都有惟一的温度与之对应，t是自变量，T因变量(T是t的函数)．

　 在上述的2个问题中，s＝30t，给出变量t的一个值，就可以得到变量s惟一值与之对应，t是自变量，s因变量(s是t的函数)。

　　 在上述的第3个问题中，V＝2πR²，给出变量R的一个值，就可以得到变量V惟一值与之对应，R是变量，V因变量(V是R的函数)．

　　 在上述的第4个问题中，lf＝300000，即l＝，给出一个f的值，就可以得到变量l惟一值与之对应，f是自变量，l因变量(l是f的函数)。函数的概念：如果在-个变化过程中；有两个变量，假设X与Y，对于X的每一个值，Y都有惟一的值与它对应，那么就说X是自变量，Y是因变量，此时也称 Y是X的函数．

　　 要引导学生在以下几个方面加对于函数概念的理解．

　　 变化过程中有两个变量，不研究多个变量；对于X的每一个值，Y都有唯一的值与它对应，如果Y有两个值与它对应，那么Y就不是X的函数。例如y²＝x

1．常量和变量

　　 在上述两个问题中有几个量?分别指出两个问题中的各个量?

　　 第1个问题中，有两个变量，一个是时间，另一个是温度，温度随着时间的变化而变化．

　　 第2个问题中有路程s，时间t和速度v，这三个量中s和t可以取不同的数值是变量，而速度30千米/时，是保持不变的量是常量．路程随着时间的变化而变化。

　　 第3个问题中的体积V和R是变量，而　是常量，体积随着底面半径的变化而变化．

　　 第4个问题中的l与频率f是变量．而它们的积等于300000，是常量．

　　 常量：在某一变化过程中始终保持不变的量，称为常量．

　　 变量：在某一变化过程中可以取不同数值的量叫做变量．