3．△ABC∽△A′B′c′，相似比为，已知△A′B′C′的面积为18cm²，那么 △ABC的面积为(　　　　 )。

2．相似三角形对应角平分线比为0.2，则相似比为(　　　 )，周长比为(　　 )，面积比为(　　　 )

1.△ABC∽△A′B′C′，相似比为3:2，则对应中线的比等于(　　 )。

上述两个三角形会相似，它们对应边的比就是相似比，△ABC∽△A′B′C′，相似比为＝2

相似的两个三角形，它们的对应角相等，对应边会成比例，除此之外，还会得出什么结果呢?

　　 一个三角形内有三条主要线段；高、中线、角平分线。如果两个三角形相似，那么这些对应的线段有什么关系呢?我们先探索一下它们的对应高之间的关系。

　　 同学画出上述的两个三角形，作对应边AB和A′B′边上的高，用刻度尺量一量CD与C′D′的长，等于多少呢?与它们的相似比相等吗?得出结论：

　　 相似三角形对应高的比等于相似比。我们能否用说理的方法来说明这个结论呢?同学们用上面类似方法，得出：相似三角形对应中线的比等于相似比；相似三角形对应角平分线的比等于相似比。　　

　　 两个相似三角形的周长比会等于相似比吗?

　　 两个相似三角形的面积之间有什么关系呢?

看如图的三个三角形，三角形(2)的各边长分别是(1)的2倍，(3)的各边长分别是(1)的3倍，所以它们都是相似的，填空：

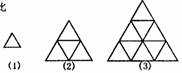
　　 (2)与(1)的相似比为(　　 )，(2)与(1)的面积比为(　　　 )，

　　 (3)与(1)的相似比为(　　 )，(3)与(1)的面积比为(　　　 )

　　 (3)与(2)的相似比为(　　 )，(3)与(2)的面积比为(　　　 )。

　　 以上可以看出当相似比为K时，面积比为K2。对于一般相似的三角形都具有这种关系，可以得出结论：相似三角形的面积比等于相似比的平方。

2．在△ABC与△A′B′C′中，AB＝l0cm，AC＝6cm，BC＝8cm，A′B′＝5cm，A′C′＝3cm，B′C′＝4cm，这两个三角形相似吗?说明理由。

如果相似，它们的相似比是多少?

1．识别两个三角形相似的简便方法有哪些?

P82　2

3．相似三角形的性质

教学目标

　 会说出相似三角形的性质：对应角相等，对应边成比例，对应中线、角平分线、高的比等于相似比，周长比等于相似比，面积比等于相似比的平方。

教学过程

到现在我们学习了识别两个三角形是否相似的三种较简便的方法，请同学回忆说出．

课本78页练习1、2，3．

2．如图△ABC中，D、E是AB、AC上点，AB＝7.8，AD＝3，AC＝6，CE＝2.1，试判断△ADE与△ABC是否会相似，小张同学的判断理由是这样的：

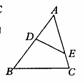　　 解：因为AC＝AE+CE，而AC＝6，CE＝2.1，

　　 故　 AE＝6-2.1＝3.9

　 　由于≠

　　 所以△ADE与△ABC不会相似。

　　 你同意小张同学的判断吗?请你说说理由。

　　 小张同学的判断是错误的。

　　 因为＝，＝＝　所以＝

而　 ∠A是公共角，∠A＝∠A，

　　 所以△ADE∽△ACB．　　

　　 请同学再做一次实验，看看如果两个三角形的三条边都成比例，那么这两个三角形是否相似?

　　 看课本77页“做一做”．

　　 通过实验得出：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．简单说成：三边成比例两三角形相似。

例:△ABC和△A′B′C′中，AB＝6cm，BC＝8cm，AC＝l0cm，A′B′＝18cm，B′C′＝24cm，A′C′＝30cm，试判定它们是否相似，并说明理由．