
16.如图,以AB为直径的⊙O与直线CD相切于点E,且AC⊥CD,BD⊥CD,
AC=8 cm,BD=2 cm,则四边形ACDB的面积为______.
[提示]设AC交⊙O于F,连结BF.
∵ AB为⊙O的直径,
∴ ∠AFB=90°.
连结OE,则OE⊥CD,
∴ AC∥OE∥BD.
∵ 点O为AB的中点,
∴ E为CD的中点.
∴ OE=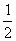 (BD+AC)=
(BD+AC)=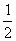 (8+2)=5(cm).
(8+2)=5(cm).
 ∴ AB=2×5=10(cm).
∴ AB=2×5=10(cm).
在Rt△BFA中,AF=CA-BD=8-2=6(cm),AB=10 cm,
∴ BF= =8(cm).
=8(cm).
∴ 四边形ACDB的面积为
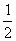 (2+8)·8=40(cm2).
(2+8)·8=40(cm2).
[答案]40 cm2.
[点评]本题考查直径的性质、中位线的判定与性质、切线的性质.注意:在圆中不要忽视直径这一隐含条件.
5.已知两圆的半径分别为3和7,圆心距为5,则这两个圆的公切线有_____条.
[提示]∵ 7-3<5<7+3,
∴ 两圆相交,
∴ 外公切线有2条,内公切线有0条.
[答案]2.
[点评]本题考查两圆的位置关系及对应的圆心距与两圆半径的关系.注意:仅仅从
5<7+3并不能断定两圆相交,还要看5与7-3的大小关系.
14.用铁皮制造一个圆柱形的油桶,上面有盖,它的高为80厘米,底面圆的直径为50厘米,那么这个油桶需要铁皮(不计接缝) 厘米2(不取近似值).
[提示]铁皮的面积即圆柱的侧面积与两底的面积的和.底面圆面积为 p·502=625p(厘米2),底面圆周长为p×50=50p(厘米),则铁皮的面积为2×625p+80×50p=5250p(厘米2).
p·502=625p(厘米2),底面圆周长为p×50=50p(厘米),则铁皮的面积为2×625p+80×50p=5250p(厘米2).
[答案]5250p厘米2.
[点评]本题考查圆柱的侧面展开图的面积及圆柱的表面积.注意:圆柱的表面积等于侧面积与两底面积之和.
13.如图,在△ABC中,AB=AC,∠C=72°,⊙O过A、B两点,且与BC切于点B,
与AC交于D,连结BD,若BC=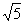 -1,则AC=______.
-1,则AC=______.
[提示]在△ABC中,AB=AC,
则 ∠ABC=∠ACB=72°,
∴ ∠BAC=36°.
 又 BC切⊙O于B,
又 BC切⊙O于B,
∴ ∠A=∠DBC=36°.
∴ ∠BDC=72°.
∴ ∠ABD=72°-36°=36°.
∴ AD=BD=BC.
易证△CBD∽△CAB,
∴ BC 2=CD·CA.
∵ AD=BD=BC,
∴ CD=AC-AD=AC-BC.
∴ BC2=(AC-BC)·CA.
解关于AC的方程,得AC= BC.
BC.
∴ AC= ·(
·(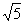 -1)=2.
-1)=2.
[答案]2.
[点评]本题考查弦切角定理、等腰三角形的性质、相似三角形的性质.注意底角为72°的等腰三角形的特殊性,底角的平分线把对边分成的两线段的比为 ,即成黄金比.
,即成黄金比.
12.已知四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形的中位线长为_____.
[提示]圆外切四边形的两组对边之和相等,则上、下底之和为10,故中位线长为5.
[答案]5.
[点评]本题考查圆外切四边形的性质.注意:本题还可求得圆外切等腰梯形的腰长也为5,即等于中位线长.
11.已知⊙O1和⊙O2的半径分别为2和3,两圆相交于点A、B,且AB=2,则
O1O2=______.

[提示]当两圆在AB的两侧时,设O1O2交AB于C,则O1O2⊥AB,且AC=BC,
∴ AC=1.
在Rt△AO2C中,O2C= =
= =2
=2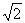 ;
;
在Rt△AO1C中,O1C= =
= =
= .
.
∴ O1O2=2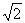 +
+ .
.
当两圆在AB的同侧时,同理可求O1O2=2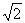 -
- .
.
[答案]2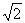 ±
± .
.
[点评]此题考查“两圆相交时,连心线垂直于公共弦”的应用.注意:在圆中不要漏解,因为圆是轴对称图形,符合本题条件的两圆有两种情形.
10.如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB
为直径的半圆围成的图形的面积为S2,则S1与S2的关系是………………………( )
(A)S1>S2 (B)S1<S2 (C)S1=S2 (D)S1≥S2

[提示]设OA=a,则S1=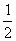 a2,弓形ACB的面积=
a2,弓形ACB的面积= pa2-
pa2-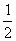 a2.
a2.
在Rt△AOB中,AB=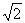 a,则以AB为直径的半圆面积为
a,则以AB为直径的半圆面积为
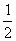 ·p·(
·p·( )2=
)2=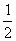 p·(
p·( a)2=
a)2= pa2.则S2=
pa2.则S2= pa2-(
pa2-( pa2-
pa2-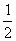 a2)=
a2)=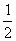 a2.
a2.
[答案]C.
[点评]本题考查三角形、圆、弓形的面积计算.注意:弓形的面积计算方法.
9.一个圆锥的侧面积是底面积的2倍,则这个圆锥的侧面展开图的圆周角是……( )
(A)60° (B)90° (C)120° (D)180°
[提示]设圆锥的母线长为a,圆心角度数为n,底面圆的半径为r,则

解此方程组,得 n=180.
[答案]D.
[点评]此题考查圆锥的侧面展开图的概念.注意理解圆柱、圆柱的侧面展开图的有关概念.
8.两圆半径之比为2︰3,当两圆内切时,圆心距是4厘米,当两圆外切时,圆心距为( )
(A)5厘米 (B)11厘米 (C)14厘米 (D)20厘米
[提示]设两圆半径分别为2 x、3 x厘米,则内切时有3 x-2 x=4,所以x=4.于是两圆半径分别为8厘米、12厘米.故外切时圆心距为20厘米.
[答案]D.
[点评]本题考查两圆内切、外切时,圆心距与两圆半径的关系.注意:要理解并记忆两圆的五种位置关系及圆心距与半径的关系.
7.一个扇形的弧长为20p 厘米,面积是240p 厘米2,则扇形的圆心角是……………( )
(A)120° (B)150° (C)210° (D)240°
[提示]设扇形的圆心角为n度,半径为R,则 解方程组得
解方程组得
[答案]B.
[点评]本题考查扇形的弧长、面积公式.注意:应熟记扇形的弧长公式、扇形的面积公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com