
25.解:根据题意得70(100-10x).x%=168,x2-10x+24=0,解得 x1=6, x2=4,
当x2=4时,100-10×4=60>50,不符合题意,舍去, x1=6时,100-10×6=40<50,
∴税率应确定为6%.
点拨:这是有关现实生活知识应用题,是近几年中考题的重要类型, 要切实理解,掌握.
24.解:设小张每小时加工x个零件,则小李每小时加工x+1个,
根据题意得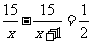 ,解得 x1=-6(舍), x2=5.
,解得 x1=-6(舍), x2=5.
所以小张每小时加工5个零件,只要符合条件就行,本题是开放性题目,答案不惟一.
23.解:如答图,易证△ABC∽△ADC,
∴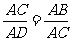 ,AC2=AD·AB.同理BC2=BD×AB,
,AC2=AD·AB.同理BC2=BD×AB,
∴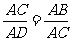 ,
,
∵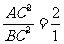 ,
,
∴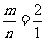 ,∴m=2n ①.
,∴m=2n ①.
∵关于x的方程 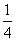 x2-2(n-1)x+m2-12=0有两实数根,
x2-2(n-1)x+m2-12=0有两实数根,
∴△=[-2(n-1)2-4×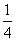 ×(m2-12)≥0,
×(m2-12)≥0,
∴4n2-m2-8n+16≥0,
把①代入上式得n≤2 ②.
设关于x的方程 x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
则x1+x2=8(n-1), x1·x2=4(m2-2),
依题意有(x1-x2)2<192, 即[8(n-1)]2-4(m2-12)]<192,
∴4n2-m2-8n+4<0,把①式代入上式得n>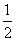 ③,由②、③得
③,由②、③得 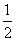 <n≤2,
<n≤2,
∵m、n为整数,∴n的整数值为1,2,
当n=1,m=2时,所求解析式为y=2x+1,当n=2,m=4时,解析式为y=4x+2.
22.(1)证明:方程x2+2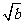 x+2c-a=0有两个相等的实根,
x+2c-a=0有两个相等的实根,
∴△=0,即△=(2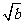 )2-4×(2c-a)=0,
)2-4×(2c-a)=0,
解得a+b=2c,方程3cx+2b=2a的根为0,则2b=2a,a=b,
∴2a=2c,a=c,
∴a=b=c,故△ABC为等边三角形.
(2)解:∵a、b相等,∴x2+mx-3m=0有两个相等的实根,
∴△=0,∴△=m2+4×1×3m=0,
即m1=0,m2=-12.
∵a、b为正数,
∴m1=0(舍),故m=-12.
21.k=-3,y2-20y-21=0
解:(1)由题意得x1+x2=k+2, x1·x2=2k+1, x12+x22=(x1+x2)2-2 x1·x2=k2+2,又x12+x22=11,
∴k2+2=11,k=±3,
当k=3时,△=-3<0, 原方程无实数解;当k=-3时,△=21>0,原方程有实数解,故k=-3.
(2)当k=-3时, 原方程为x2+x-5=0,设所求方程为y2+py+q=0,两根为y1,y2,
则y1=x1+x2=-1,y2=(x1-x2)2=x12+x22-2x1x2=11+10=21,
∴y1+y2=20,y1y2=-21,故所求方程是y2-20y-21=0.
点拨:要求k的值,须利用根与系数的关系及条件x12+x22=(x1+x2)2-2 x1·x2,构造关于k的方程,同时,要注意所求出的k值,应使方程有两个实数根,即先求后检.
(2)构造方程时,要利用p=-(y1+y2),q=y1y2,则以y1,y2为根的一元二次方程为y2+py+q=0.
20.60,30 解:设宽为xcm,则长为2xcm,由题意得(2x-10)×(x-10)×5=1500,
解得x1=20,x2=-5(舍去),2x=40. 本题注意单位要一致.
19.4083 点拨:由公式法得x=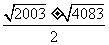 ,则
,则
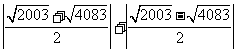 =
=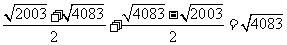
∴A2=4083
18.a+β≥1 点拨:方程有实根,则△≥0,则k≤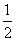 , 即-k≥-
, 即-k≥-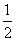 ,1-k≥1-
,1-k≥1-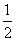 ,2(1-k)≥1,∵a+β=2(1-k),∴a+β≥1.
,2(1-k)≥1,∵a+β=2(1-k),∴a+β≥1.
17.x2+7x+12=0或x2-7x+12=0 点拨:设两数为a,b,则ab=12,a2+b2=25,
∴( a+b)2-2ab=25,(a+b)2=49,(a+b)=±7,
所以以a,b为根的方程为x2+7x+12= 0 或x2-7x+12=0.
16.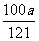 元 点拨:设原价x元,则x(1+10%)2=a,解得x=
元 点拨:设原价x元,则x(1+10%)2=a,解得x=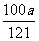 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com