6．若圆锥的底面半径为 3，母线长为5，则它的侧面展开图的圆心角等于　　　　 (　)

A．　　 108°　　 B．　　 144°　　 C．　　 180°　　 D．　 216°

5．在Rt△ABC中，已知AB＝6，AC＝8，∠A＝90°，如果把此直角三角形绕直线AC旋转一周得到一个圆锥，其表面积为S₁；把此直角三角形绕直线AB旋转一周得到另一个圆锥，其表面积为S₂，那么S₁∶S₂等于　　　　　　　　　　　　　　　　　　　 (　)

A　　 2∶3　 　B　　 　3∶4　 　C　　 4∶9　 　D　　 5∶12

4．如图，两个等圆⊙O和⊙O′外切，过O作⊙O′的两条切线OA、OB，A、B是切点，则∠AOB等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

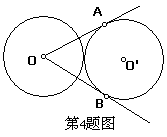A.　 　30° 　　　　B.　　　 45°　　　 C.　　 　60°　　　　 D.　　　 90°　

3．在直角坐标系中,以O(0，0)为圆心,以5为半径画圆,则点A(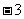,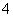)的位置在　　　 (　　 )

A　　　 ⊙O内　　　 B　　　 ⊙O上　　 C　　　 ⊙O外　　　 D　　 不能确定

2．半径相等的圆内接正三角形、正方形、正六边形的边长之比为　　　　　　　　 (　)

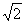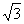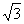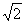A　　 1∶2∶3　 　B 　1∶∶　 C 　∶∶1　 D 　　3∶2∶1

1．如图，直角三角形ABC中，∠C＝90°，AC＝2，AB＝4，分别以AC、BC为直径作半圆，则图中阴影的面积为　　　　　　　　　　　　　　 　　　　　　　　(　)

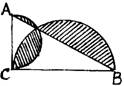
A　　 2π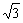－　 B　 4π－4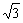　

C　　 5π－4　　 D　 2π－2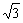

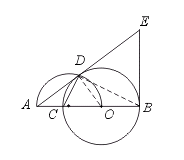
30．(14分)如图，已知O是线段AB上一点，以OB为半径的⊙O交线段AB于点C，

以线段OA为直径的半圆交⊙O于点D，过点B作AB垂线与AD的延长线交于点E，

连结CD．若AC＝2，且AC、AD的长是关于x的方程x²－kx+4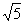＝0的两个根．

(1)证明AE切⊙O于点D；

(2)求线段EB的长；

(3)求tan ∠ADC的值．

[提示]连结OD、BD．(1)证∠ODA＝90°即可；(2)利用切割线定理，结合一元二次方程根与系数的关系求BE的长；(3)利用相似三角形的比进行转化．

(1)[略证]连结OD．

∵　 OA是半圆的直径，∴　 ∠ADO＝90°．∴　 AE切⊙O于点D．

(2)[略解]∵　 AC、AD的长是关于x的方程x²－kx+4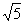＝0的两个根，且AC＝2，AC·AD＝2，

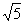∴　 AD＝4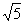．∵　 AD是⊙O的切线，ACB为割线，

∴　 AD²＝AC·AB．又　 AD＝2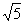，AC＝2，∴　 AB＝10．

则　BC＝8，OB＝4．∵　 BE⊥AB，

∴　 BE切⊙O于B．

又　 AE切⊙O于点D，∴　 ED＝EB．

在Rt△ABE中，设BE＝x，由勾股定理，得

(x+2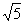)²＝x²+10²．

解此方程，得　 x＝4．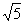

即BE的长为4．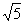

(3)连结BD，有∠CDB＝90°．

∵　 AD切⊙O于D，

∴　 ∠ADC＝∠ABD，且tan ∠ADC＝tan ∠ABD＝．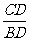

在△ADC和△ABD中，∠A＝∠A，∠ADC＝∠ABD，

∴　 △ADC∽△ABD．

∴　 ＝＝＝．

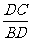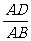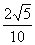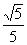∴　 tan ∠ADC＝．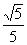

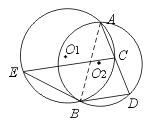
29．(12分)如图，已知CP为⊙O的直径，AC切⊙O于点C，AB切⊙O于点D，并

与CP的延长线相交于点B，又BD＝2 BP．

求证：(1)PC＝3 PB；(2)AC＝PC．

[提示](1)因为BC＝BP+PC，所以要证PC＝3 BP，即要证BC＝4 BP，用切割线定理进行转化．(2)要证AC等于⊙O的直径，即要证AC＝2×半径．只要连结OD，易证△BOD∽△BAC．可利用相似三角形的性质证明结论．

[略证](1)∵　 BD是⊙O的切线，BPC是⊙O的割线，

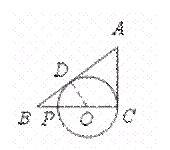∴　 BD²＝BP·BC．

∵　 BD＝2 BP，∴　 4 BD²＝BP·BC．

∴　 4 BP＝BC．∵　 BC＝BP+PC，

∴　 4 BP＝BP+PC．∴　 PC＝3 BP．

(2)连结DO．

∵　 AB切⊙O于点D，AC切⊙O于点C，

∴　 ∠ODB＝∠ACB＝90°．

∵　 ∠B＝∠B，∴　 △ODB∽△ACB．

∴　 ＝＝＝．

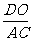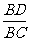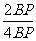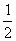∴　 AC＝2 DO．∴　 PC＝2 DO．∴　 AC＝PC．

[点评]此题体现了圆幂定理和切线性质定理的应用，解题的关键是善于转化．

28．(8分)已知：如图(1)，⊙O₁与⊙O₂相交于A、B两点，经过A点的直线分别交⊙O₁、⊙O₂于C、D两点(C、D不与B重合)，连结BD，过点C作BD的平行线交⊙O₁于点E，连BE．

(1)求证：BE是⊙O₂的切线；

(2)如图(2)，若两圆圆心在公共弦AB的同侧，其他条件不变，判断BE和⊙O₂的位置关系(不要求证明)．

[提示](1)过B作⊙O₂的直径BH，连结AB、AH，证∠EBH＝90°．(2)用类似的方法去探求．

[证明](1)连结AB，作⊙O₂的直径BH，连结AH．

则　 ∠ABH+∠H＝90°，∠H＝∠ADB，∠EBA＝∠ECA．

∵　 EC∥BD，

∴　 ∠ADB＝∠ACE＝∠EBA．

∴　 ∠EBA+∠ABH＝90°．

即　 ∠EBH＝90°．

∴　 BE是⊙O₂的切线．

(2)同理可知，BE仍是⊙O₂的切线．

[点评]证明一与圆有公共点的直线是圆的切线的一般方法是过公共点作半径(或直径)，再证直径与半径垂直，但此题已知条件中无90°的角，故作直径构造90°的角，再进行角的转换．同时两圆相交，通常作它们的公共弦，这样把两圆中的角都联系起来了．另外，当问题进行了变式时，要学会借鉴已有的思路解题．

27．(8分)如图，⊙O表示一个圆形工件，图中标注了有关尺寸，且MB︰MA＝1︰4，

求工件半径的长．

[提示]把OM向两方延长，交⊙O于点C、D．设⊙O的半径为R，则可用相交弦定理求半径长．

[略解]把OM向两方延长，分别交⊙O于C、D两点．设⊙O的半径为R．

从图中知，AB＝15 cm．

又　 MB︰MA＝1︰4，

∴　 MB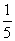＝×15＝3(cm)，MA＝12 cm．

从图中知，CM＝R+8，MD＝R－8，

由相交弦定理，得　 AM·BM＝CM·MD．

∴　 12×3＝(R+8)(R－8)．

解此方程，得　 R＝10或R＝－10(舍去)．

故工件的半径长为10 cm．

[点评]此题是一道实际问题，要善于把实际问题转化为数学问题，因在圆中，OM与AB相交，故向相交弦定理转化．