
3.设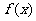 在
在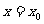 处可导,且
处可导,且 ,则
,则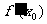 等于( )
等于( )
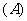 1
1
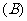
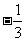
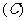

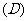
2.关于函数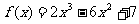 ,下列说法不正确的是
( )
,下列说法不正确的是
( )
 在区间
在区间 内,
内,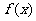 为增函数
为增函数 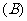 在区间
在区间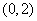 内,
内,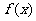 为减函数
为减函数
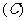 在区间
在区间 内,
内,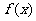 为增函数
为增函数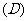 在区间
在区间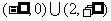 内
内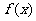 为增函数
为增函数
1.函数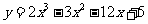 在[0,3]上的最大值与最小值分别是 ( )
在[0,3]上的最大值与最小值分别是 ( )
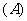
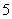 、
、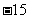
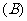
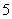 、
、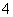
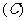
 、
、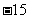
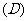
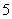 、
、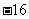
例1.若函数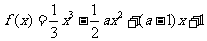 在区间
在区间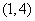 内为减函数,在区间
内为减函数,在区间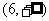 上为增函数,试求实数
上为增函数,试求实数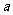 的取值范围.
的取值范围.
解: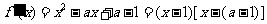 ,
,
令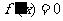 得
得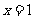 或
或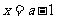 ,
,
∴当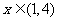 时,
时,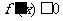 ,当
,当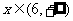 时,
时,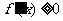 ,
,
∴ ,∴
,∴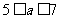 .
.
例2.已知函数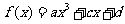
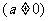 是
是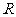 上的奇函数,当
上的奇函数,当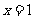 时
时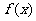 取得极值
取得极值 ,
,
(1)求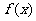 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意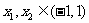 ,不等式
,不等式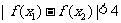 恒成立.
恒成立.
解:(1)由奇函数的定义,应有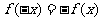 ,
,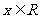 ,
,
即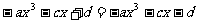 ,∴
,∴ 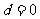 ,∴
,∴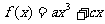 ,∴
,∴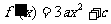 ,由条件
,由条件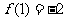 为
为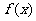 的极值,必有
的极值,必有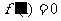 ,故
,故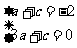 ,
,
解得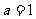 ,
,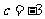 ,∴
,∴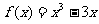 ,
,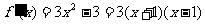 ,
,
∴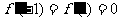 ,
,
当 时,
时,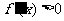 ,故
,故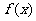 在单调区间
在单调区间 上是增函数;
上是增函数;
当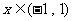 时,
时,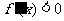 ,故
,故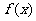 在单调区间
在单调区间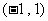 上是减函数;
上是减函数;
当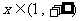 时,
时,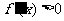 ,故
,故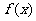 在单调区间
在单调区间 上是增函数,
上是增函数,
所以,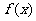 在
在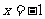 处取得极大值,极大值为
处取得极大值,极大值为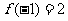 .
.
(2)由(1)知,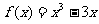
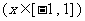 是减函数,
是减函数,
且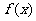 在
在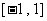 上的最大值
上的最大值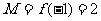 ,最小值
,最小值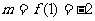 ,
,
所以,对任意的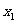 ,
,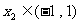 ,恒有
,恒有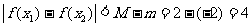 .
.
例3.设函数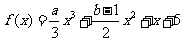
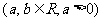 的定义域为
的定义域为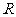 ,当
,当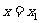 时,取得极大值;当
时,取得极大值;当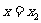 时取得极小值,
时取得极小值,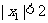 且
且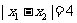 .
.
(1)求证: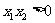 ;(2)求证:
;(2)求证: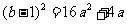 ;(3)求实数
;(3)求实数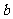 的取值范围.
的取值范围.
(1)证明: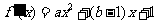 ,
,
由题意,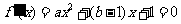 的两根为
的两根为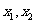 ,∴
,∴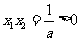 .
.
(2)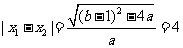 ,∴
,∴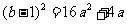 .
.
(3)①若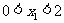 ,则
,则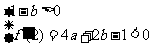 ,
,
∴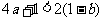 ,从而
,从而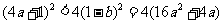 ,
,
解得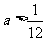 或
或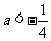 (舍)
(舍)
∴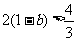 ,得
,得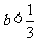 .
.
②若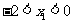 ,则
,则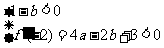 ,
,
∴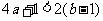 ,从而
,从而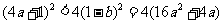 ,
,
解得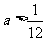 或
或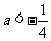 (舍)
(舍)
∴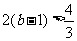 ,∴
,∴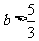 ,
,
综上可得,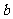 的取值范围是
的取值范围是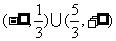 .
.
小结:本题主要考查导数、函数、不等式等基础知识,综合分析问题和解决问题的能力.
5.若对任意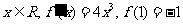 ,则
,则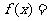
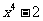 .
.
4.已知函数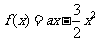 的最大值不大于
的最大值不大于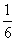 ,又当
,又当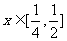 时,
时,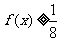 ,则
,则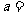 1.
1.
3.若曲线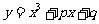 与
与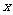 轴相切,则
轴相切,则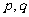 之间的关系满足(
之间的关系满足( 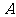 )
)
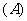
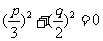
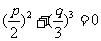
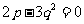
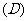
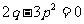
2.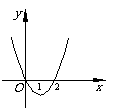 设
设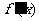 是函数
是函数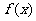 的导函数,
的导函数,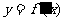 的图象如下图(1)所示,则
的图象如下图(1)所示,则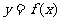 的图象最有可能的是 (
的图象最有可能的是 ( 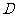 )
)
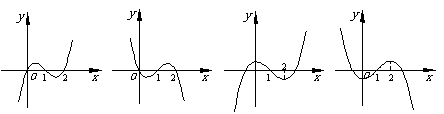 |
|||
|
|||
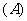
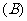
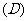
1.设函数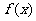 在
在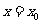 处有导数,且
处有导数,且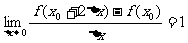 ,则
,则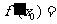 (
( )
)
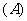 1
1 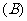 0
0 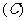 2
2 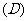
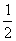
29.图13反映了美国汽车产业布局及区位选择的发展和变化,回答下列问题。(14分)
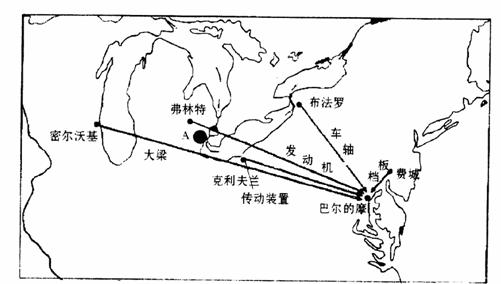
图13 汽车工业布局的变化
(1)试分析 A 城市能成为世界著名汽车城的工业区位优势条件。(3分)
(2)分析巴尔的摩发展汽车工业的优越区位条件。(3分)
(3)过去,汽车相关产业大量集中在 A 城。而现在汽车相关产业分散在各地。试比较它们各自的优势与不足。(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com