
3.教学内容详解:
◆举例说出区域的特征。
◇能归纳出区域的主要特征,并用简洁的学科科学语言表达。
◇能举出说明该区域特征的地理事象。
◆以两个区域为例,比较分析地理环境差异对区域发展的影响。
◇通过比较两个级别相当的自然区或经济区,理解由于不用区域的环境、资源、社会经济、人地关系的差异,造成发展条件的差异,最终导致经济发展的差异。
◆以某区域为例,比较分析区域不同发展阶段地理环境的影响。
◇以某一经济区为例,分析在不同的发展阶段,由于区域发展条件变化,导致的区域发展水平及经济结构的差异、人地关系的差异。
◆举例说明区域之间的联系。
◆通过两个特征差异明显的区域比较,说明区域联系的必要性。
2.课标要求:
◆了解区域的含义。
◆以长江三角洲和松嫩平原两个不同区域为例,比较自然环境、人类活动的区域差异。
◆以长江三角洲为例,比较不同发展阶段地理环境对人类生产和生活方式的影响。
1.内容综述
3. 在长方体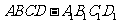 中,
中, 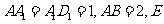 为
为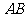 的中点, 则
的中点, 则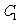 到平面
到平面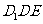 的距离为( A ) .
的距离为( A ) .
A. 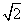 B. 2
C.
B. 2
C. 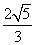 D.
D. 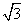
已知向量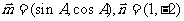 ,且
,且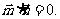
(Ⅰ)求tanA的值; (Ⅱ)求函数 R)的值域.
R)的值域.
已知函数f(x)=Asin(x+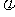 )(A>0,0<
)(A>0,0<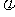 <
< ),x
),x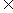 R的最大值是1,其图像经过点M
R的最大值是1,其图像经过点M .
.
(1)求f(x)的解析式;
(2)已知α,β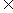
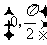 ,且f(α)=
,且f(α)=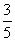 ,f(β)=
,f(β)=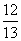 ,求f(α-β)的值.
,求f(α-β)的值.
在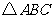 中,内角
中,内角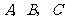 对边的边长分别是
对边的边长分别是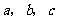 ,已知
,已知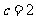 ,
,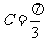 .
.
(Ⅰ)若 的面积等于
的面积等于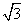 ,求
,求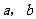 ; (Ⅱ)若
; (Ⅱ)若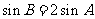 ,求
,求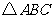 的面积.
的面积.
设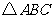 的内角
的内角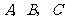 所对的边长分别为
所对的边长分别为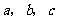 ,且
,且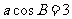 ,
,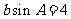 .
.
(Ⅰ)求边长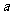 ; (Ⅱ)若
; (Ⅱ)若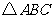 的面积
的面积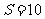 ,求
,求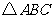 的周长
的周长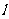 .
.
9.(2009山东卷理)将函数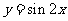 的图象向左平移
的图象向左平移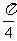 个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
A.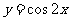 B.
B.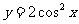 C.
C.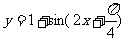 D.
D.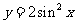
[解析]:将函数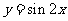 的图象向左平移
的图象向左平移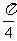 个单位,得到函数
个单位,得到函数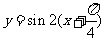 即
即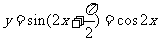 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为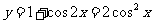 ,故选B.
,故选B.
答案:B
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式
将函数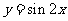 的图象向左平移
的图象向左平移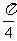 个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
A. 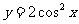 B.
B. 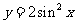 C.
C.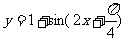 D.
D. 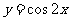
[解析]:将函数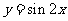 的图象向左平移
的图象向左平移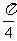 个单位,得到函数
个单位,得到函数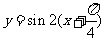 即
即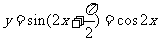 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为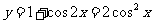 ,故选A.
,故选A.
答案:A
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
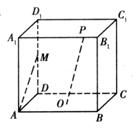 2. 如图, 在正方体
2. 如图, 在正方体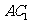 中,
中, 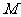 是棱
是棱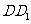 的中点,
的中点, 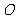 是平面
是平面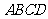 的中心,
的中心, 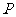 是
是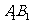 上的任意一点, 则直线
上的任意一点, 则直线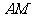 与
与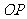 所成角是( D ) .
所成角是( D ) .
A. 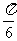 B.
B. 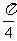 C.
C. 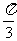 D.
D. 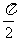
新编高考题库,立体几何,P24
4.(2009全国卷Ⅰ理)若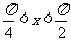 ,则函数
,则函数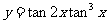 的最大值为
。
的最大值为
。
解:令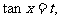
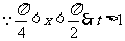 ,
, 

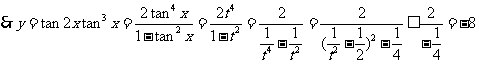


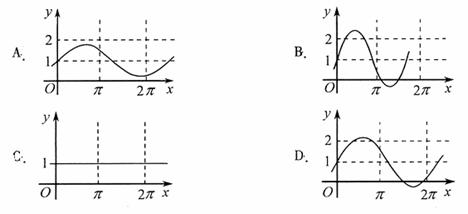
[命题意图]此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度.
[解析]对于振幅大于1时,三角函数的周期为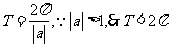 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了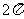 .
.
[答案]A
[解析]本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查.
当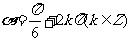 时,
时,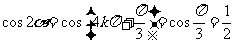 ,
,
反之,当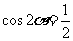 时,有
时,有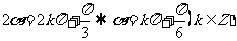 ,
,
或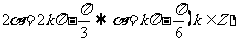 ,故应选A.
,故应选A.
6.已知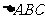 中,
中,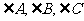 的对边分别为
的对边分别为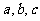 若
若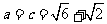 且
且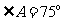 ,则
,则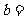
A.2 B.4+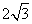 C.4-
C.4-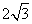 D.
D.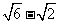
[答案]A
[解析]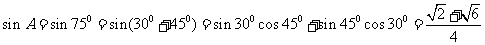
由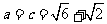 可知,
可知,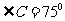 ,所以
,所以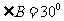 ,
,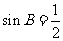
由正弦定理得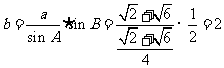 ,故选A
,故选A
5. “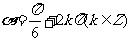 ”是“
”是“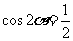 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件
4.已知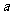 是实数,则函数
是实数,则函数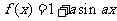 的图象不可能是( D )
的图象不可能是( D ) 

3.如果函数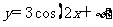 的图像关于点
的图像关于点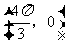 中心对称,那么
中心对称,那么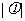 的最小值为(C)(A)
的最小值为(C)(A)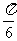 (B)
(B)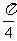 (C)
(C)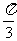 (D)
(D) 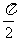

解:  函数
函数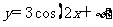 的图像关于点
的图像关于点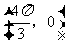 中心对称
中心对称 

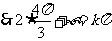
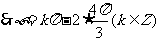 由此易得
由此易得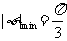 .故选C
.故选C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com