
4、文化是世界建筑世界文化里头最高的一个层次。
3、人类在认识自然和人造环境过程中,对建筑的理解常常会出现一种失去平衡的情况,这需要我们用正确的理论来纠正它。
2、建筑有使用价值、经济价值和文化价值,而各地文化形成了一个总的文化价值。应该把建筑的价值观提高到一个总的价值上来。
1、地区及地区的环境是建筑的属性。
21.解:(1) 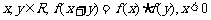 时,f(x)>1;
时,f(x)>1;
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1,
∴f(0)=1 . ……………………………2分
若x>0,则f(x-x)=f(0)=f(x)f(-x)故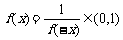 ,
,
故x∈R f(x)>0.…………………………………………………4分
任取x1<x2 ,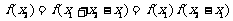 ,
,
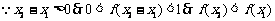 ,
,
故f(x)在R上减函数.……………………………6分
(2) ①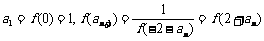 ,…………8分
,…………8分
由f(x)单调性得 an+1=an+2
, 故{an}等差数列 , 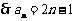 .………………9分
.………………9分
②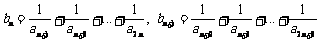 ,
,
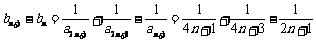
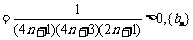 是递增数列.………………………11分
是递增数列.………………………11分
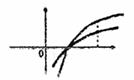 当n≥2时,
当n≥2时,
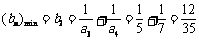 ,
,
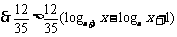 ,……………………………12分
,……………………………12分
即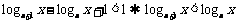 .
.
而a>1,∴x>1,
故x的取值范围(1,+∞).……………………………14分
[链接高考]本题是抽象函数与数列的综合题.近年抽象函数的考查力度有所降低,今年的高考会否有所加强值得注意,此外数列则是多年出现在高考的后两题,在复习中应适当强化数列综合题应进行系统探究,思考数列可能与哪些分支的知识综合考查值得我们关注.
20.解:(Ⅰ)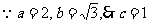 .
…..1分
.
…..1分
椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0);…..2分
而抛物线的焦点坐标为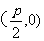 即得p=2,所以所求抛物线的方程为
即得p=2,所以所求抛物线的方程为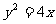 .…..5分
.…..5分
(Ⅱ)证明:设M,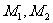 的坐标分别为
的坐标分别为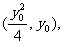
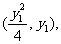
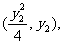
由A、M、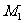 三点共线得:
三点共线得: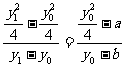 , …..7分
, …..7分
化简得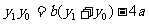 ,
,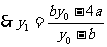 ;
;
同理,由B、M、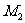 三点共线得:
三点共线得: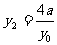 . …..9分
. …..9分
设(x,y)是直线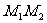 上的任意一点,则
上的任意一点,则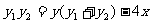 ; …..10分
; …..10分
把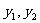 代入上式整理得:
代入上式整理得: ;
;
由M是任意的,则有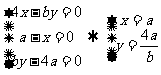 , …..13分
, …..13分
所以动直线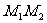 恒过定点
恒过定点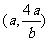 . …..14分
. …..14分
[链接高考]圆锥曲线和直线是解析几何的主线,考查学生的运算能力是解析几何的重要部分,特别是包含比较多字母的运算,同时也考查了“设而不求”的解题策略和数形结合的数学思想方法.
19.解:(1)依题意知:直线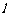 是函数
是函数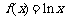 在点
在点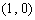 处的切线,
处的切线,
故其斜率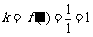 ,所以直线
,所以直线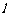 的方程为
的方程为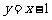 .…………………2分
.…………………2分
因为直线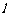 与
与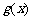 的图像相切,
的图像相切,
所以由 ,…………………4分
,…………………4分
得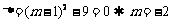 (
(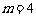 不合题意,舍去);…………………5分
不合题意,舍去);…………………5分
(2)因为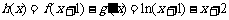 (
( ),
),
所以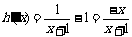 .
…………………7分
.
…………………7分
当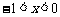 时,
时,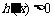 ;当
;当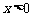 时,
时,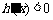 .…………………8分
.…………………8分
因此,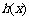 在
在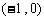 上单调递增,在
上单调递增,在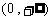 上单调递减.…………………9分
上单调递减.…………………9分
因此,当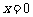 时,
时,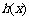 取得最大值
取得最大值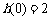 ;…………………10分
;…………………10分
(3)当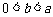 时,
时,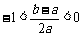 .
.
由(2)知:当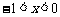 时,
时,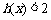 ,即
,即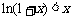 .…………………12分
.…………………12分
因此,有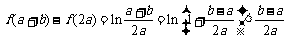 .…………………14分
.…………………14分
[链接高考]导数是高中数学课程中的重要内容,是解决实际问题的强有力的数学工具,运用导数的有关知识,研究函数的性质(单调性、极值和最值)是高考的热点问题。本题中的(2)的结论对(3)的解决有承上启下的作用,这也是高考常见的考查方式,值得注意。
18.解:(1)证明:
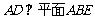 ,
,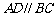 ,
,
∴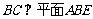 ,则
,则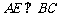 . ……2分
. ……2分
又
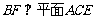 ,则
,则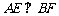 ,
,
∴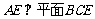 .
.
又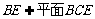 , ∴
, ∴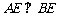 . ……4分
. ……4分
(2)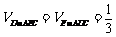 ×
×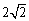 ×
×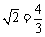 .
……8分
.
……8分
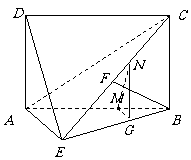
(3)在三角形ABE中过M点作MG∥AE交BE于G点,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,则
由比例关系易得CN=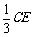 ,
…………………9分
,
…………………9分
 MG∥AE
MG
MG∥AE
MG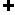 平面ADE, AE
平面ADE, AE 平面ADE,
平面ADE,
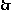 MG∥平面ADE .
…………………10分
MG∥平面ADE .
…………………10分
同理,
GN∥平面ADE,又MG∩GN=G,MG 平面MGN,GN
平面MGN,GN 平面MGN
平面MGN
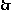 平面MGN∥平面ADE .
…………………12分
平面MGN∥平面ADE .
…………………12分
又MN 平面MGN ,
平面MGN , 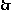 MN∥平面ADE.
MN∥平面ADE.
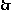 N点为线段CE上靠近C点的一个三等分点. …………………14分
N点为线段CE上靠近C点的一个三等分点. …………………14分
[链接高考]本题主要考查简单几何体的有关知识,以及求证线线垂直及三棱锥的体积和探求某动点在运动中的确定位置使线面平行的问题,以及分析问题与解决问题的能力.
17.解:满足条件的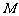 点共有
点共有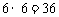 个,
…………………1分
个,
…………………1分
(1)正好在第二象限的点有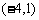 ,
,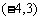 ,
,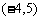 ,
,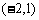 ,
,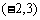 ,
,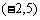 ,…………3分
,…………3分
故点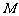 正好在第二象限的概率P1=
正好在第二象限的概率P1=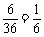 .
………………4分
.
………………4分
(2)在x轴上的点有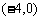 ,
,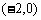 ,
,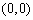 ,
,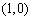 ,
,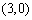 ,
,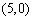 ,
……6分
,
……6分
故点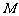 不在x轴上的概率P2=1-
不在x轴上的概率P2=1-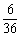 =
=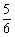 .
……………………8分
.
……………………8分
(3)在所给区域内的点有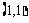 ,
,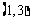 ,
,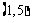 ,
,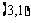 ,
,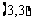 ,
,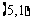 , ………10分
, ………10分
故点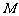 在所给区域上的概率
在所给区域上的概率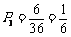 .
……………………11分
.
……………………11分
答:(1)点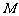 正好在第二象限的概率是
正好在第二象限的概率是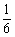 ,(2)点
,(2)点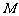 不在x轴上的概率是
不在x轴上的概率是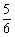 ,(3)点
,(3)点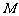 在所给区域上的概率
在所给区域上的概率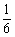 .
…………………12分
.
…………………12分
 [链接高考]概率是新课标增加的内容,近年来每年都有一道大题,这部分知识考查的力度有所增加。文科高考主要掌握古典概型与几何概型这两种概率模型以及概率的基本运算法则。本题是概率及线性规划的综合应用。
[链接高考]概率是新课标增加的内容,近年来每年都有一道大题,这部分知识考查的力度有所增加。文科高考主要掌握古典概型与几何概型这两种概率模型以及概率的基本运算法则。本题是概率及线性规划的综合应用。
16.解:(Ⅰ)由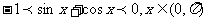 得
得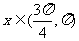 , …..2分
, …..2分
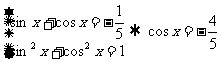 .
…..6分
.
…..6分
(Ⅱ)由(Ⅰ)得sinx=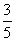
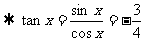 ,
…..7分
,
…..7分
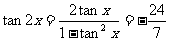 ,
…..9分
,
…..9分
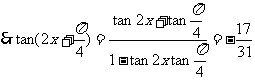 .
…..12分
.
…..12分
[链接高考]本小题是与整份试卷中三角部分相配套,侧重考查学生对三角中的基本函数-sinx,cosx,tanx的掌握程度,这也是新课程的要求.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com