
12.
⑴对物块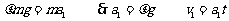
对盖: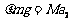
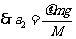
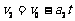
恰好分离的临界条件是: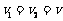
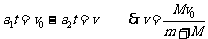
⑵恰好分离的条件: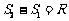 ①
①
小物块位移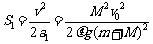
盖的位移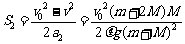
联球解得: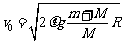
设分离点在A点,则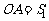
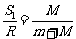
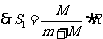 与
与 无关,可见分离点应是一个的定点,都会在同一点分离.
无关,可见分离点应是一个的定点,都会在同一点分离.
11.解:(1)设两滑块碰前A的速度为v1,由动能定理有:
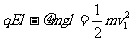 (2分)
(2分)
解得:v1=3m/s (2分)
A、B两滑块碰撞,由于时间极短动量守恒,设共同速度为v
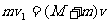 (2分)
(2分)
解得:v=1.0m/s (2分)
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理有:
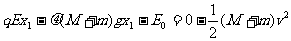 (2分)
(2分)
解得:x1=0.02m (1分)
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:
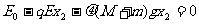 (2分)
(2分)
解得:x2≈0.05m (1分)
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离为:S=x2+s-x1=0.05m+0.05m-0.02m=0.08m. (4分)
10、(1)因为带电体到达C点时的动能最大,所以到C点时的电势能最小(电势最高),所以等势面与OC垂直,电场线的方向沿CO方向,由几何知识可得电场与AC方向成30°角。该问题也可以与力学问题进行类比来分析,如果将重力场与电场类比,小球到达C点时的动能最大,则C点相当于重力场中最低点,所以电场力的方向一定是沿OC方向。
(2)当小球恰好能打到C点时,由抛体运动的规律,
有: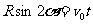 ,
,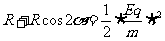 ,
,
所以初动能为: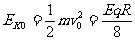 。
。
9、甲同学的错误原因:认为物体速度为零时,一定处于平衡状态,或者认为偏角最大的是平衡位置。 乙同学的错误原因:将安培力表示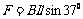 导致F做功出错。
导致F做功出错。
正解如下:铜棒向外偏转过程中,导线拉力不做功,如图丙所示。
F做功为: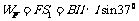 ,重力做功为:
,重力做功为: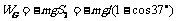
由动能定理得: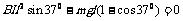 ,
,
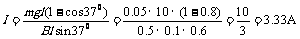
8.
解:小球第一次从O到A的过程中,由动能定理,得W+WG+WF=0
小球第二次下落到A点整个过程中,同理有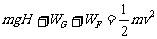
解得小球的速度为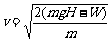
7.
(1)小球重力所做功为
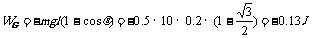 (3分)
(3分)
(2)外力F做功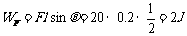 (3分)
(3分)
(3)将小球和框架槽看作一个系统,则系统动能定理: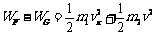 (2分)
(2分)
,其中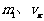 为小球的质量和小球此时的速度,
为小球的质量和小球此时的速度,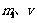 为框架槽的质量和此时的速度.
为框架槽的质量和此时的速度.
由运动的分解得: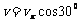 (3分)
(3分)
代入上述方程::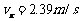 (3分)
(3分)
6.
⑴ 对整体自由落体,加速度为g; 以A为研究对象,A作自由落体则杆对A一定没有作用力。(3分)
⑵ AB都进入圆轨道后,两环具有相同角速度,则两环速度大小一定相等
整体机械能守恒: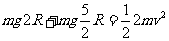
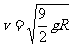 (6分)
(6分)
⑶ A再次上升后,位置比原来高h,如图所示。
由动能定理 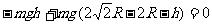
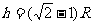 ,
,
A离开底部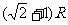 (7分)
(7分)
5、
(1)设所有物块都相对木板静止时的速度为 v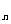 ,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
m v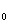 +m·2 v
+m·2 v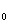 +m·3 v
+m·3 v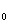 +…+m·n v
+…+m·n v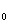 =(M + nm)v
=(M + nm)v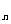 1
1
M = nm, 2
解得:
v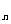 =
=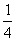 (n+1)v
(n+1)v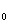 ,
6分
,
6分
(2)设第1号物块相对木板静止时的速度为v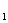 ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
木板和物块1 △p =(M + m)v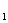 -
m v
-
m v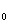 ,
,
2至n号物块 △p =(n-1)m·(v
=(n-1)m·(v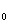 -
v
-
v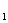 )
)
由动量守恒定律: △p=△p ,
,
解得
v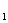 =
=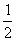 v
v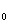 ,
3 6分
,
3 6分
(3)设第k号物块相对木板静止时的速度由v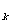 ,则第k号物块速度由k v
,则第k号物块速度由k v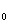 减为v
减为v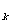 的过程中,序数在第k号物块后面的所有物块动量都减小m(k
v
的过程中,序数在第k号物块后面的所有物块动量都减小m(k
v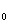 -
v
-
v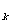 ),取木板与序号为1至K号以前的各物块为一部分,则
),取木板与序号为1至K号以前的各物块为一部分,则
△p=(M+km)v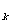 -(m v
-(m v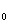 +m·2 v
+m·2 v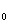 +…+mk v
+…+mk v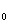 )=(n+k)m v
)=(n+k)m v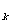 -
-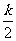 (k+1)m v
(k+1)m v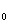
序号在第k以后的所有物块动量减少的总量为
△p =(n-k)m(k v
=(n-k)m(k v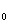 -
v
-
v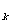 )
)
由动量守恒得
△p=△p ,
即
,
即
(n+k)m v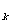 -
-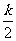 (k+1)m v
(k+1)m v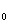 = (n-k)m(k v
= (n-k)m(k v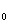 -
v
-
v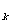 ),
),
解得 v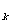 =
=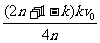 6分
6分
4、
(1)赛车由C到O,有 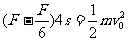 ①
2分
①
2分
车与缓冲器短时相撞过程根据动量守恒: 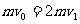 ②
2分
②
2分
O到D过程 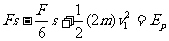 ③ 3分
③ 3分
由①②③求得: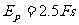 1分
1分
(2)D到O过程 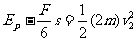 ④
2分
④
2分
赛车从O点到停止运动 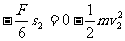 ⑤
2分
⑤
2分
车整个过程克服摩擦力做功 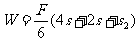 ⑥
2分
⑥
2分
由④⑤⑥求得: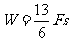 1分
1分
3、(12分)
解:(1)陈若琳跃起后可看作竖直向上的匀减速运动,重心上升的高度h1=0.45m
设起跳速度为v0,则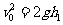 ,上升过程的时间
,上升过程的时间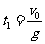
解得 t1=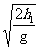 =0.3 s
(3分)
=0.3 s
(3分)
陈若琳从最高处自由下落到手触及水面的过程中重心下落的高度h=10.45m
设下落过程的时间为t2,则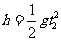
解得 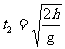 =
=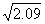 s≈1.4 s
(2分)
s≈1.4 s
(2分)
陈若琳要完成一系列动作可利用的时间t=t1+t2=1.7s (1分)
说明:t2用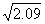 s表示也给分。
s表示也给分。
(2)陈若琳的手触及水面到她的重心下沉到离水面约2.2m处的位移s=3.0 m
手触及水面时的瞬时速度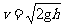 (2分)
(2分)
设水对运动员的作用力为Ff,依据动能定理有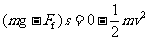 (2分)
(2分)
解得 Ff=1.3´103N (2分)
说明:用其他方法求解,正确的也给分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com