
4.已知函数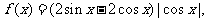 则函数
则函数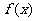 的最大值是
( )
的最大值是
( )
A.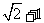 B.
B.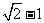 C.
C.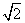 D.2
D.2
3.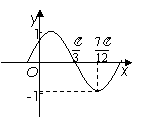 把函数
把函数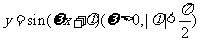 的图象向左平移
的图象向左平移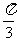 个单位,所得曲线的一部分如图所示,则
个单位,所得曲线的一部分如图所示,则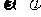 的值分别为
( )
的值分别为
( )
A. 2,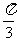 B. 2,
B. 2,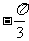
C. 1,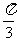 D. 1,
D. 1,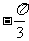
2.已知角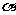 的终边上一点的坐标为
的终边上一点的坐标为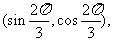 则角
则角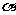 的最小正值为
( )
的最小正值为
( )
A.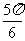 B.
B.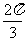 C.
C.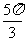 D.
D. 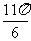
1.若集合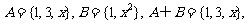 则满足条件的实数x的个数有 ( )
则满足条件的实数x的个数有 ( )
A. 1个 B. 2个 C.3个 D. 4个
21.(本小题满分14分)
解:(Ⅰ)由条件知a2-a1=―2,a3―a2=―1;
∵{an+1-an}是等差数列, ∴首项a2―a1=―2,公差d=(a3―a2)―(a2―a1)=1;
∴an+1―an=―2+(n―1)d=n―3. …………………2分
当n≥2时,
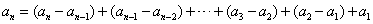
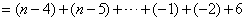
=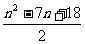 ;
;
当n=1时也满足, ∴n∈N*,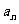 =
=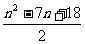 . …………………5分
. …………………5分
∵{bn―2}是等比数列,首项b1―2=4,b2―2=2,∴公比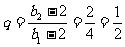 ;
;
∴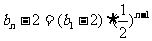 ,
,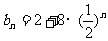 . …………………8分
. …………………8分
(Ⅱ)设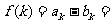
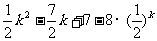 =
=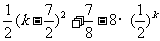 ,
,
当k≥4时,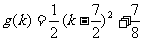 为
为 的单增函数,
的单增函数,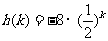 也为
也为 的单增函数,
的单增函数,
∴k≥4时,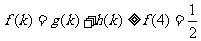 .…………………12分
.…………………12分
∵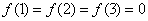 , ∴不存在k∈N*,使存在k∈N*,使
, ∴不存在k∈N*,使存在k∈N*,使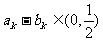 .
.
…………………14分
20.(本小题满分14分)
解:(Ⅰ)由题意可知直线l的方程为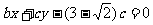 ,
,
因为直线与圆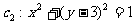 相切,所以
相切,所以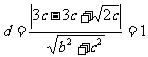 ,即
,即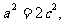
从而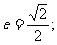 …………………6分
…………………6分
(Ⅱ)设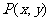 、圆
、圆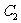 的圆心记为
的圆心记为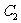 ,则
,则
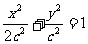 (
(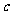 ﹥0),又
﹥0),又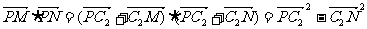 =
=
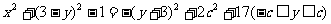 . …………………8分
. …………………8分
j当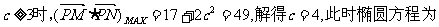
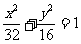 ;
;
k当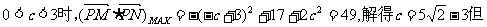
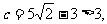 故舍去.
故舍去.
综上所述,椭圆的方程为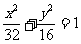 .
…………………14分
.
…………………14分
19.(本小题满分14分)
解:(Ⅰ)∵ 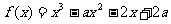 ,
,
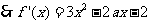 …………………2分
…………………2分
(Ⅱ)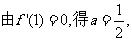
则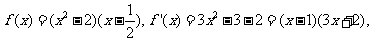
令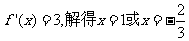 .
…………………5分
.
…………………5分
当x在区间[-1,2]上变化时,y’,y的变化情况如下表:
|
X |
-1 |
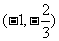 |
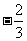 |
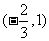 |
1 |
(1,2) |
2 |
|
Y’ |
|
+ |
0 |
- |
0 |
+ |
|
|
Y |
3/2 |
单增 |
极大值 |
单减 |
极小值 |
单增 |
3 |
又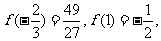
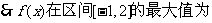
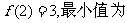
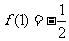 . …………………9分
. …………………9分
(Ⅲ)证明: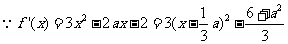 ,
,
又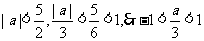 ,
,
 .
.
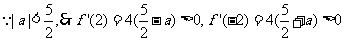 ,
,
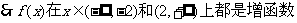 . …………………14分
. …………………14分
18.(本小题满分13分)
解:(Ⅰ)由题设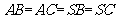
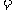
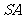 ,连结
,连结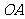 ,
,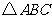 为等腰直角三角形,
为等腰直角三角形,
所以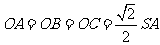 ,且
,且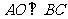 ,又
,又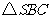 为等腰三角形,
为等腰三角形,
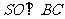 ,且
,且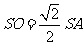 ,从而
,从而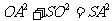 .
.
所以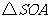 为直角三角形,
为直角三角形,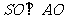 .
.
又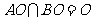 . 所以
. 所以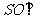 平面
平面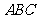 .
…………………6分
.
…………………6分
(Ⅱ)由(Ⅰ)知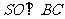 ,
,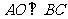 ,
,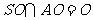 得,
得,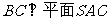 ;
;
而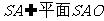 ,所以
,所以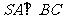 .
…………………10分
.
…………………10分
(Ⅲ) 易知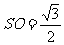 ,
,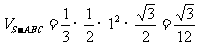 . ………………13分
. ………………13分
17.(本小题满分13分)
解:(Ⅰ)甲、乙二人抽到的牌的所有基本事件(方块4用4’表示,下同)为
(2,3),(2,4),(2,4),(3,2),(3,4),(3,4’),(4,2),(4,3),(4,4’),(4’,2),
(4’,3),(4’,4)共12种不同情况.--------(4分)
 (Ⅱ)甲抽到3,乙抽到的牌只能是2,4,4’.
(Ⅱ)甲抽到3,乙抽到的牌只能是2,4,4’.
因此,乙抽到的牌的数字大于3的概率是 .
…………………7分
.
…………………7分
(Ⅲ)甲抽到牌比乙大有(3,2),(4,2),(4,3),(4’,2),(4’,3)共5种,所以,甲胜的概率是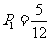 ,乙获胜的与甲获胜是对立事件,所以乙获胜的概率是
,乙获胜的与甲获胜是对立事件,所以乙获胜的概率是 ,
,
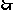 此游戏不公平.
…………………13分
此游戏不公平.
…………………13分
16.(本小题满分12分)
解:(Ⅰ)由题设及正弦定理知: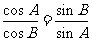 ,得
,得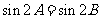 ,
,
∴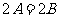 或
或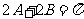 ,即
,即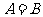 或
或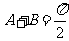 .
.
当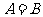 时,有
时,有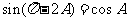 , 即
, 即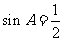 ,得
,得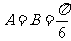 ,
,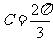 ;
;
当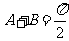 时,有
时,有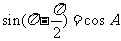 ,即
,即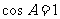 ,不符题设,
,不符题设,
∴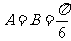 ,
,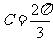 . …………………7分
. …………………7分
(Ⅱ) 由(Ⅰ)及题设知: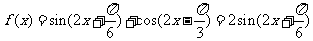 ;
;
当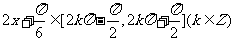 时,
时, 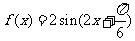 为增函数,
为增函数,
即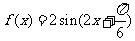 的单调递增区间为
的单调递增区间为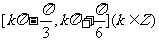 . ………11分
. ………11分
它的相邻两对称轴间的距离为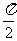 . ………12分
. ………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com