
11.不等式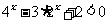 的解集是
的解集是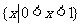 .
.
[解]由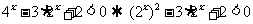
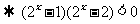
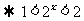 .
.
所以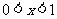 ,故不等式的解集是
,故不等式的解集是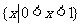 .
.
10.博才实验中学共有学生1600名,为了调查学生的身体健康状况,采用分层抽样法抽取一个容量为200的样本.已知样本容量中女生比男生少10人,则该校的女生人数是 760 人.
[解]设该校女生人数为,则男生人数为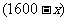 .
.
由已知,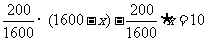 ,解得
,解得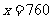 .故该校的女生人数是760人.
.故该校的女生人数是760人.
9.设全集U={0,1,2,3,4},集合A={0,a},B={3,4},若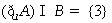 ,则a的值为 4
.
,则a的值为 4
.
[解]显然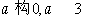 ,检验知,只有当a=4时才符合条件.
,检验知,只有当a=4时才符合条件.
8.已知定义在R上的函数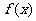 满足:对任意x∈R,都有
满足:对任意x∈R,都有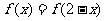 成立,且当
成立,且当 时,
时, (其中
(其中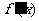 为
为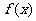 的导数).设
的导数).设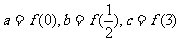 ,则a,b,c三者的大小关系是
( B )
,则a,b,c三者的大小关系是
( B )
A. 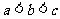 B.
B.
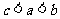 C.
C.
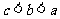 D.
D.
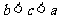
[解]由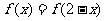 可得,函数
可得,函数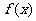 的图象关于直线
的图象关于直线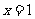 对称,所以
对称,所以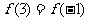 .
.
又当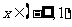 时,
时, ,即
,即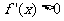 ,则
,则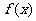 在
在 上单调递增.
上单调递增.
所以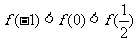 .即
.即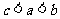 ,故选B.
,故选B.
7.已知曲线C的参数方程是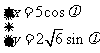 (为参数),则曲线C上的点P到定点M(-2,0)的最大距离是
( C )
(为参数),则曲线C上的点P到定点M(-2,0)的最大距离是
( C )
A.9 B. 8 C. 7 D. 6
[解]解法一:因为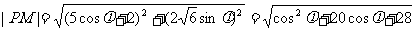
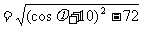 ,所以当
,所以当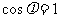 时,
时,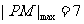 ,故选C.
,故选C.
解法二:将曲线C的参数方程化为普通方程,得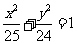 ,它表示焦点在x轴上的椭圆.由椭圆的几何性质可知,当点P位于椭圆的右顶点时,|PM|为最大,且最大值为5+2=7,故选C.
,它表示焦点在x轴上的椭圆.由椭圆的几何性质可知,当点P位于椭圆的右顶点时,|PM|为最大,且最大值为5+2=7,故选C.
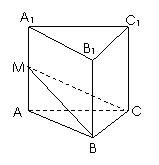
6.如图,在正三棱柱ABC-A1B1C1中,点M为侧棱AA1上
一动点,已知△BCM面积的最大值是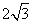 ,二面角M―BC―A
,二面角M―BC―A
的最大值是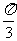 ,则该三棱柱的体积等于
( A )
,则该三棱柱的体积等于
( A )
A. 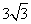 B.
B. 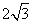 C.
C. 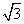 D.
D. 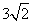
[解]当点M与点A1重合时,△BCM的面积为最大值,此时二面角M―BC―A也为最大.
由已知可得,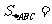
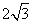
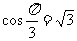 ,所以底面正三角形ABC 的边长为2,高为
,所以底面正三角形ABC 的边长为2,高为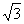 ,从而正三棱柱的高AA1=
,从而正三棱柱的高AA1=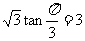 .所以正三棱柱的体积
.所以正三棱柱的体积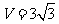 ,故选A.
,故选A.
5.函数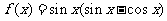 的单调递减区间是
( D )
的单调递减区间是
( D )
A.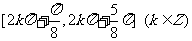 B.
B. 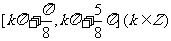
C.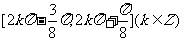 D.
D.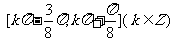
[解]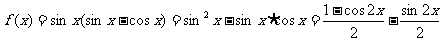
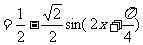 .
.
由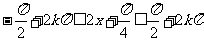 ,得
,得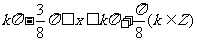 ,故选D.
,故选D.
4.某单因素单峰试验的因素范围是[10,110],用黄金分割法来确定试点,则第一个试点的值是 ( C )
A. 16.18 B. 55.62 C. 71.8 D. 61.8
[解]据黄金分割法原理,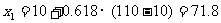 ,故选C.
,故选C.
3.“函数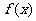 为奇函数”是“
为奇函数”是“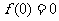 ”的
( D )
”的
( D )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
[解]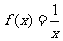 为奇函数,但
为奇函数,但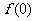 不存在;对函数
不存在;对函数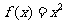 ,有
,有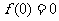 ,但
,但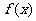 为偶函数,故选D.
为偶函数,故选D.
2.在等比数列{an}中,已知a3=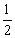 ,a9=8,则a5·a6·a7的值为
( A )
,a9=8,则a5·a6·a7的值为
( A )
A.±8 B.-8 C. 8 D.64
[解]因为{an}为等比数列,则a62=a5·a7=a3·a9=4,所以a6=±2,a5·a6·a7=±8,故选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com