
2.下列四组词语中没有错别字的一组是( )
A.望风披糜 忧心忡忡 即来之,则安之 世外桃园
B.糜糜之音 纵横驰聘 弥天大谎 人才辈出
C.兵荒马乱 戍马倥偬 仓遑逃窜 箭拔弩张
D.寻物启事 莫名其妙 沧桑巨变 山清水秀
1.给下列加点字注音:
犭严 狁之故( )( ) 不遑启居( ) 我戍未定( )
王事不盬( ) 小人所腓( ) 靡使归聘( )
23. 选修4-4:坐标系与参数方程.
选修4-4:坐标系与参数方程.
在直角坐标系xoy中,以o为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为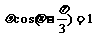 ,M,N分别为C与x轴,y轴的交点
,M,N分别为C与x轴,y轴的交点
(1)写出C的直角坐标方程,并求出M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程
解:(1)将极坐标方程为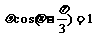 化为:
化为: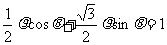
则其直角坐标方程为: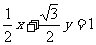 ,
,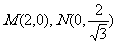 ,其极坐标为
,其极坐标为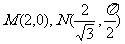
(2)其中点P(1,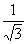 )
)
OP的直线方程为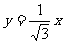 ,化为极坐标方程为:
,化为极坐标方程为: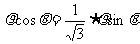
化简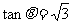 ,即极坐标方程为
,即极坐标方程为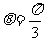 。
。
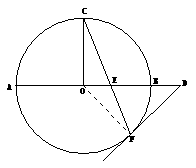
22.选修4-1:几何证明选讲.
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB
过F点作⊙O的切线交AB的延长线于D.连结CF交AB于E点.
(1)求证: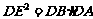 ;
;
(2)若⊙O 的半径为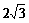 ,OB=
,OB=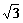 OE,求EF 的长.
OE,求EF 的长.
(1)证明:∵DF是切线,∴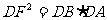
又∠DEF=∠CEO=900-∠ECO=900-∠EFO=∠DFE
∴DE=DF
∴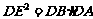
(2)由相交弦定理:CE·EF=AE·EB
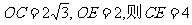
又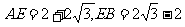 ,∴
,∴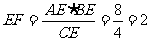
21. (本小题14分)
(本小题14分)
 已知函数
已知函数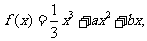 且
且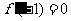
 (I)试用含
(I)试用含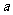 的代数式表示
的代数式表示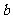 ;
;
 (Ⅱ)求
(Ⅱ)求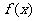 的单调区间;
的单调区间;
 (Ⅲ)令
(Ⅲ)令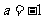 ,设函数
,设函数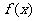 在
在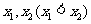 处取得极值,记点
处取得极值,记点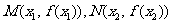 ,证明:线段
,证明:线段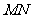 与曲线
与曲线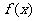 存在异于
存在异于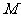 、
、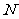 的公共点.
的公共点.
解:(1)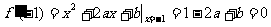 ,即b=2a-1
,即b=2a-1
(2)由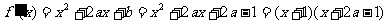 =0
=0
①a>1时,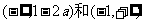 为增区间,
为增区间,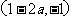 为减区间;
为减区间;
②a=1时,函数在R上为增函数;
③a<1时,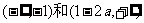 为增区间,
为增区间,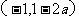 为减区间;
为减区间;
(3)证明: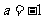 时,
时, ,
,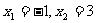 ,得
,得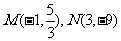
则MN: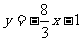 ,由方程
,由方程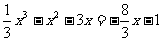 化简得:
化简得: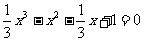
易知,x=-1,x=3,x=1是方程的根,即线段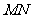 与曲线
与曲线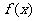 存在异于
存在异于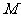 、
、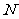 的公共点(1,-
的公共点(1,-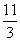 ).
).
20. (本小题12分)
(本小题12分)
 已知函数
已知函数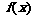 对任意实数
对任意实数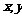 恒有
恒有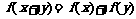 且当x>0,
且当x>0,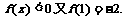
 (1)判断
(1)判断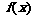 的奇偶性和单调性;
的奇偶性和单调性;
 (2)求
(2)求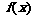 在区间[-3,3]上的最值;
在区间[-3,3]上的最值;
 (3) 解不等式
(3) 解不等式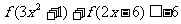 .
.
 解:(1)令x=y=0,则
解:(1)令x=y=0,则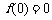 ,令y=-x,则
,令y=-x,则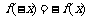 ,函数为奇函数;
,函数为奇函数;
 设
设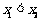 ,则
,则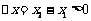 ,由已知
,由已知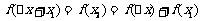 ,
,
 所以
所以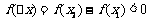 ,即函数为减函数;
,即函数为减函数;
 (2)由
(2)由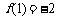 及
及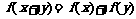 ,得
,得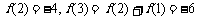
 由奇函数
由奇函数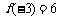 ,即函数在[-3,3]上的最值为-6和6.
,即函数在[-3,3]上的最值为-6和6.
18. (本小题10分)数列
(本小题10分)数列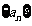 中,
中,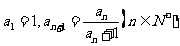 .
.
 (1)求证:数列{
(1)求证:数列{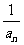 }是等差数列;
}是等差数列;
 (2)求通项
(2)求通项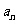 ;
;
 (1)证明:由
(1)证明:由 ,得:
,得: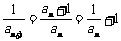 ,即:
,即:

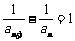 ,则数列{
,则数列{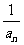 }是等差数列;
}是等差数列;
 (2)
(2)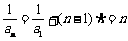 ,所以
,所以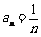 。
。
 19.(本小题12分)已知命题
19.(本小题12分)已知命题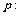
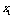 和
和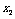 是方程
是方程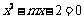 的两个实根,不等式
的两个实根,不等式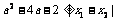 对任意实数
对任意实数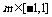 恒成立;命题
恒成立;命题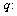 只有一个实数
只有一个实数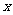 满足不等式
满足不等式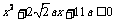 ,若命题
,若命题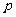 是假命题,命题
是假命题,命题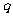 是真命题,求
是真命题,求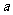 的取值范围。
的取值范围。
 解:(1)
解:(1)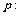
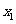 和
和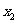 是
是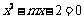 的两根,所以
的两根,所以

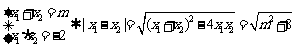
 又
又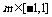 ,则有
,则有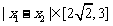 。因为不等式
。因为不等式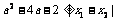 对任意实数
对任意实数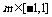 恒成立,所以
恒成立,所以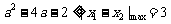 ,所以
,所以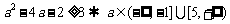

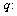 由题意有
由题意有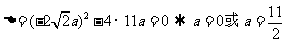
 由命题
由命题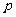 假
假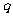 真,所以
真,所以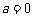 。
。

17. (本小题10分) 若函数
(本小题10分) 若函数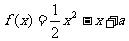 的定义域和值域均为[1,b](b>1),求a,b的值。
的定义域和值域均为[1,b](b>1),求a,b的值。
 解:因函数
解:因函数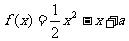 的对称轴为
的对称轴为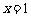 ,故在定义域[1,b](b>1)内单调递增,
,故在定义域[1,b](b>1)内单调递增,
 所以最小值
所以最小值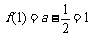 ,所以
,所以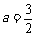 ;最大值
;最大值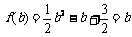 ,则b=3或1(舍)。
,则b=3或1(舍)。
13. 1 14.
1 14.
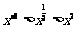 15.
15.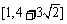 16.
16.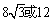


|
16. 椭圆
椭圆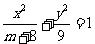 的离心率是
的离心率是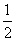 ,则椭圆两准线间的距离为
。
,则椭圆两准线间的距离为
。
 答题页(请将选择题和填空题答案填写在相应题号处,考试结束后只交此卷)
答题页(请将选择题和填空题答案填写在相应题号处,考试结束后只交此卷)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com