
5、已知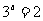 ,那么
,那么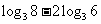 用
用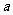 表示是( )
表示是( )
A、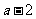 B、
B、 C、
C、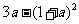 D、
D、 
4、已知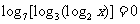 ,那么
,那么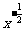 等于
等于
A、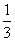 B、
B、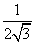 C、
C、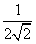 D、
D、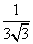
3、函数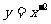 在区间
在区间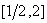 上的最大值是
上的最大值是
A、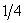 B、
B、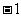 C、
C、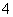 D、
D、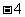
2、下列各式正确的是:
A、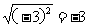 B、
B、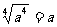 C、
C、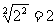 D、
D、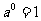
1、下列所给出的函数中,是幂函数的是
A、 B、
B、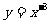 C、
C、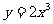 D、
D、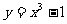
4.[解析]我们可以先假设存在这样的抛物线,如果能够求出对应的值,则存在,如果求不出,则不存在.
[答案](1)∵ 平移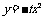 的图象得到的抛物线F的顶点为Q,
的图象得到的抛物线F的顶点为Q,
∴ 抛物线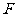 对应的解析式为:
对应的解析式为: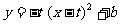 .
.
∵ 抛物线与x轴有两个交点,∴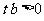 .
.
令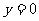 , 得
, 得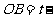
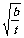 ,
,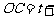
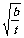 ,
,
∴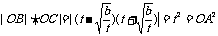
即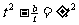 , 所以当
, 所以当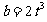 时, 存在抛物线F使得
时, 存在抛物线F使得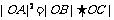 .
.
(2) ∵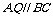 ,∴
,∴ 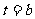 ,得F:
,得F:
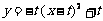 ,
,
解得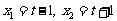
在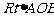 中,
中,
1) 当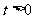 时,由
时,由 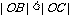 , 得
, 得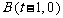 ,
,
当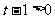 时, 由
时, 由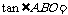
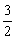
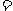
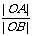
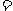
 ,
,
解得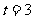 ,
,
此时, 二次函数解析式为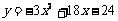 ;
;
当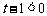 时, 由
时, 由
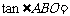
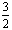 =
=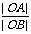 =
=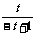 , 解得
, 解得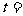
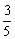 ,
,
此时,二次函数解析式为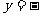
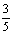
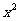 +
+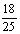
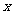 +
+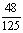 .
.
2) 当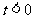 时, 由
时, 由 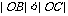 , 将
, 将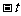 代
代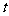 , 可得
, 可得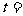
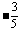 ,
, 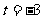 ,
,
(也可由 代
代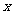 ,
,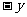 代
代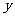 得到)
得到)
所以二次函数解析式为 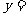
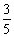
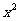 +
+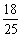
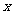 –
–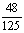 或
或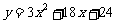 .
.
3.[解析]解决在产品的营销过程中如何获得最大利润的“每每型”试题成为近年中考的热点问题。每每型”试题的特点就是每下降,就每减少,或每增长,就每减少。解决这类问题的关键就是找到单价降低后,该商场每天的销售量。“每每型”试题都可以转化为二次函数最值问题,利用二次函数的图像和性质加以解决.
[答案](1)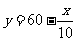
(2)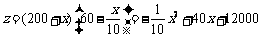
(3)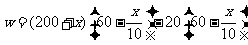
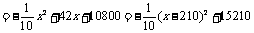
当x=210时,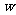 有最大值.
有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时,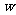 有最大值,且最大值是15210元.
有最大值,且最大值是15210元.
2.[解析]先建立函数关系式,把它转化为二次函数的一般形式,然后根据二次函数的顶点坐标公式进行求极值.
[答案]解:设增种x棵树,果园的总产量为y千克,依题意得:y=(100 + x)(40 – 0.25x ) =4000 – 25x + 40 x – 0,25x2 = - 0.25 x2 + 15x + 4000
因为a= - 0.25<0,所以当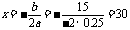 ,
,
y有最大值
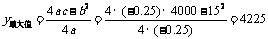
答:增种30棵枇杷树,投产后可以使果园枇杷的总产量最多,最多总产量是4225千克.
1.[解析]从函数图象容易看出前面一段是出台该项优惠政策前的情况,后面一段是出台该项优惠政策后的情况,前面一段所有的量已经知道,容易求出该果园共销售脐橙的重量,为后面一段的求值奠定了基础.
[答案]解:(1)政策出台前的脐橙售价为
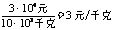 ;
;
(2)设剩余脐橙为x吨,则
103×(3×9+0.2)x=11.7×104
∴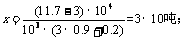
该果园共销售了10 +30 = 40吨脐橙 ;
(3)①设这个一次函数的解析式为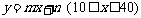 ,
,
代入两点(10,3)、(40,11.7)
得: 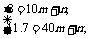
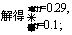 函数关系式为
函数关系式为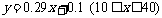 ,
,
②令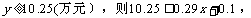
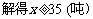
答:(1)原售价是3元/千克;(2)果园共销售40吨脐橙;(3)①函数关系式为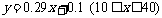 ;
;
②今年至少要销售35吨,总收入才达到去年水平.
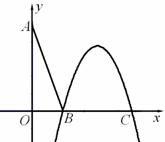
4.(•杭州市)在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
(1)是否存在这样的抛物线F,使得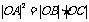 ?请你作出判断,并说明理由;
?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=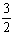 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
第2课时 函数型问题 答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com